
用Python (scikit-learn) 做PCA分析
我的上一个教程讨论了使用Python的逻辑回归(https://towardsdatascience.com/logistic-regression-using-python-sklearn-numpy-mnist-handwriting-recognition-matplotlib-a6b31e2b166a)。我们学到的一件事是,你可以通过改变优化算法来加速机器学习算法的拟合。加速机器学习算法的一种更常见的方法是使用主成分分析 Principal Component Analysis (PCA)。如果你的学习算法太慢,因为输入维数太高,那么使用PCA来加速是一个合理的选择。这可能是PCA最常见的应用。PCA的另一个常见应用是数据可视化。
为了理解使用PCA进行数据可视化的价值,本教程的第一部分介绍了应用PCA后对IRIS数据集的基本可视化。第二部分使用PCA来加速MNIST数据集上的机器学习算法(逻辑回归)。
现在,让我们开始吧!
本教程中使用的代码如下所示:“
PCA的数据可视化的应用
用PCA来加速机器学习的计算
PCA在数据可视化的应用
对于许多机器学习应用程序来说,能够可视化你的数据是很有帮助的。将2维或3维数据可视化并不那么困难。然而,即使在本教程的这一部分中使用的Iris数据集也是四维的。你可以使用主成分分析将四维数据减少到2维或3维这样你就能更好地绘制并理解数据。
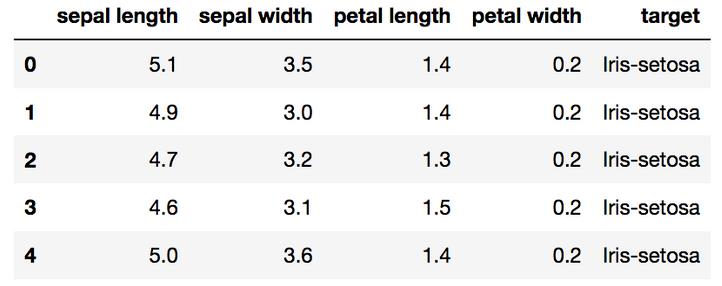
加载Iris数据集
Iris数据集是scikit-learn附带的数据集之一,不需要从外部网站下载任何文件。下面的代码将加载iris数据集。
import pandas as pd
url = “https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data”
# load dataset into Pandas DataFrame
df = pd.read_csv(url, names=[‘sepal length’,’sepal width’,’petal length’,’petal width’,’target’])
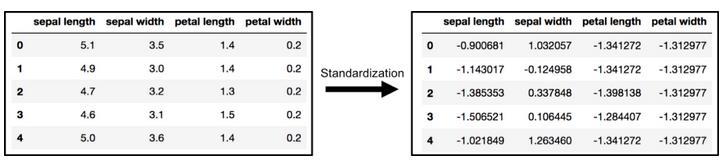
标准化数据
主成分分析受尺度影响,所以在应用主成分分析之前,需要对数据中的特征进行尺度分析。使用StandardScaler帮助你将数据集的特性标准化到单元尺度(均值= 0,方差= 1),这是许多机器学习算法实现最佳性能的要求。如果你想看到不缩放数据可能带来的负面影响,scikit-learn有一节是讲关于不标准化数据的影响的(https://scikit-learn.org/stable/auto_examples/preprocessing/plot_scaling_importance.html#sphx-glr-auto-examples-preprocessing-plot-scaling-importance-py)。
from sklearn.preprocessing
import StandardScalerfeatures = [‘sepal length’, ‘sepal width’, ‘petal length’, ‘petal width’]
# Separating out the features
x = df.loc[:, features].values
# Separating out the target
y = df.loc[:,[‘target’]].values
# Standardizing the features
x = StandardScaler().fit_transform(x)
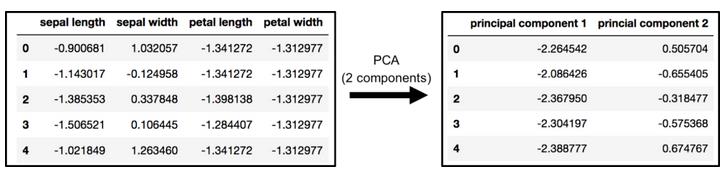
主成分分析二维“投影”
原始数据有4列(萼片长度、萼片宽度、花瓣长度和花瓣宽度)。在本节中,代码将原来的4维数据“投影”到2维中。我要指出的是,在降维之后,通常不会给每个主成分赋予一个特定的意义。新的成分只是变化的两个主要维度。
from sklearn.decomposition
import PCApca = PCA(n_components=2)
principalComponents = pca.fit_transform(x)
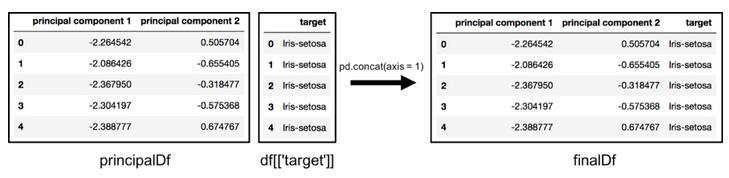
principalDf = pd.DataFrame(data = principalComponents
, columns = [‘principal component 1’, ‘principal component 2’])
finalDf = pd.concat([principalDf, df[[‘target’]]], axis = 1)
通过设置axis=1连接dataframe。finalDf是绘制数据之前的最后一个dataframe。
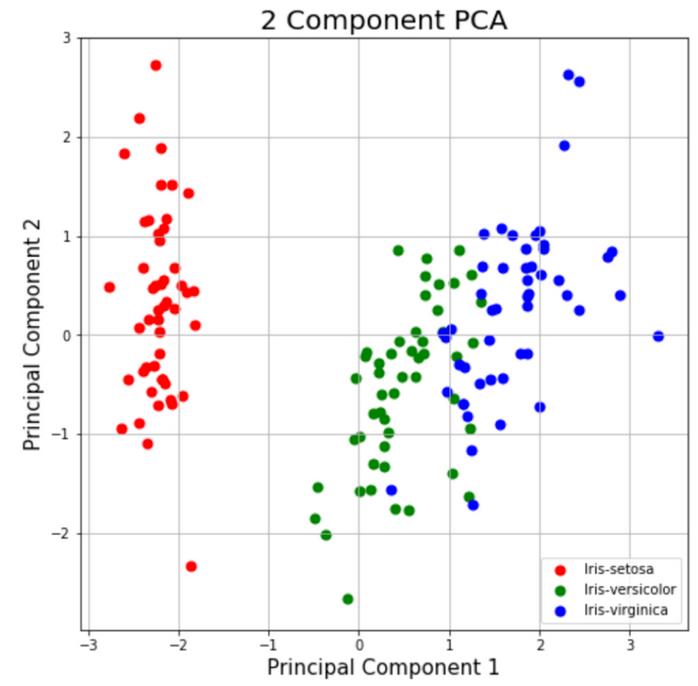
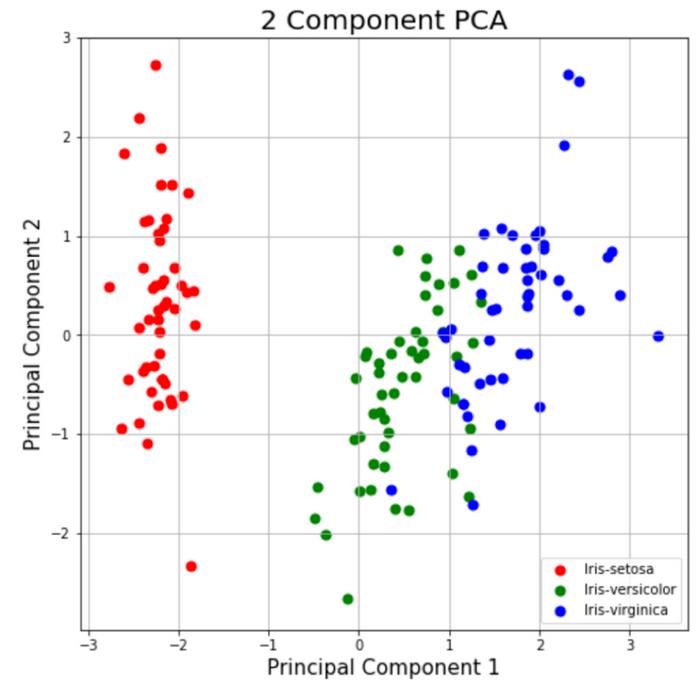
可视化二维”投影”
这部分只是绘制二维数据。请注意下面的图表,这些类似乎彼此分离得很好。
fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel(‘Principal Component 1’, fontsize = 15)
ax.set_ylabel(‘Principal Component 2’, fontsize = 15)
ax.set_title(‘2 component PCA’, fontsize = 20)
targets = [‘Iris-setosa’, ‘Iris-versicolor’, ‘Iris-virginica’]
colors = [‘r’, ‘g’, ‘b’]
for target, color in zip(targets,colors):
indicesToKeep = finalDf[‘target’] == target
ax.scatter(finalDf.loc[indicesToKeep, ‘principal component 1’]
, finalDf.loc[indicesToKeep, ‘principal component 2’]
, c = color
, s = 50)
ax.legend(targets)
ax.grid()
被解释的方差
被解释的方差告诉你有多少信息(方差)可以归因于每个主成分。这很重要,因为当你把四维空间转换成二维空间时,你会丢失一些方差(信息)。通过使用属性explained_variance_ratio_,你可以看到第一个主成分包含了72.77%的方差,第二个主成分包含了23.03%的方差。这两个部分总共包含了95.80%的信息。
pca.explained_variance_ratio_
PCA加速机器学习算法
PCA最重要的应用之一是加速机器学习算法。在这里使用IRIS数据集是不切实际的,因为该数据集只有150行和4个特征列。MNIST手写数字数据库更合适,因为它有784个特征列(784个维度)、一组包含60,000个示例的训练集和一组包含10,000个示例的测试集。
下载并加载数据
还可以向fetch_mldata添加data_home参数,以更改下载数据的位置。
from sklearn.datasets import fetch_openmlmnist = fetch_openml(‘mnist_784’)
你下载的图像包含在MNIST中。数据和形状(70000, 784)意味着有70000张具有784个维度(784个特征)的图像。标签(整数0-9)包含在mnist.target中。功能是784维(28 x 28图像)和标签只是从0到9的数字。
将数据分解为训练集和测试集
一般来说,训练测试分为80%的训练和20%的测试。在这个例子中,我选择了6/7的数据作为训练,1/7的数据作为测试集。
from sklearn.model_selection import train_test_split
# test_size: what proportion of original data is used for test set
train_img, test_img, train_lbl, test_lbl = train_test_split( mnist.data, mnist.target, test_size=1/7.0, random_state=0)
标准化数据
这一段的文字几乎完全是早先所写内容的翻版。主成分分析受尺度影响,因此在应用主成分分析之前,需要对数据中的特征进行尺度分析。你可以将数据转换到单位尺度(均值= 0和方差= 1),这是许多机器学习算法的最优性能的要求。StandardScaler帮助标准化数据集的特性。注意,你适合于训练集,并在训练和测试集上进行转换。如果你想了解不缩放数据可能带来的负面影响,scikit-learn有一节介绍不标准化数据的影响(https://scikit-learn.org/stable/auto_examples/preprocessing/plot_scaling_importance.html#sphx-glr-auto-examples-preprocessing-plot-scaling-importance-py)。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# Fit on training set only.
scaler.fit(train_img)
# Apply transform to both the training set and the test set.
train_img = scaler.transform(train_img)
test_img = scaler.transform(test_img)
导入并应用PCA
注意,下面的代码使用.95作为成分数量参数。这意味着scikit-learn选择主成分的最小数量,这样95%的方差被保留。
from sklearn.decomposition import PCA
# Make an instance of the Model
pca = PCA(.95)
在训练集中安装主成分分析。注意:你只在训练集中安装主成分分析。
pca.fit(train_img)
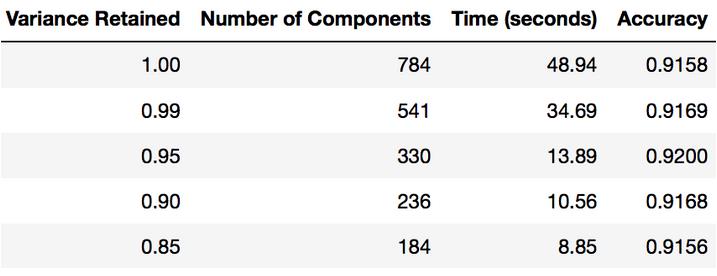
注意:通过使用pca.n_components_对模型进行拟合,可以知道PCA选择了多少个成分。在这种情况下,95%的方差相当于330个主成分。
将“映射”(转换)应用到训练集和测试集。
train_img = pca.transform(train_img)
test_img = pca.transform(test_img)
对转换后的数据应用逻辑回归
步骤1:导入你想要使用的模型
在sklearn中,所有的机器学习模型都被用作Python class。
from sklearn.linear_model import LogisticRegression
步骤2:创建模型的实例。
#未指定的所有参数都设置为默认值
#默认解算器非常慢,这就是为什么它被改为“lbfgs”
logisticRegr = LogisticRegression(solver = ‘lbfgs’)
步骤3:在数据上训练模型,存储从数据中学习到的信息
模型学习的是数字和标签之间的关系
logisticRegr.fit(train_img, train_lbl)
步骤4:预测新数据(新图像)的标签
使用模型在模型训练过程中学习到的信息
下面的代码预测了一个观察结果
#预测一次观测(图片)
logisticRegr.predict(test_img[0].reshape(1,-1))
下面的代码一次预测了多个观察结果
#预测一次观测(图片)
logisticRegr.predict(test_img[0:10])
测量模型的性能
虽然准确度并不总是机器学习算法的最佳度量标准(精度、回忆、F1分数、ROC曲线等会更好(https://towardsdatascience.com/receiver-operating-characteristic-curves-demystified-in-python-bd531a4364d0 ),但这里使用它是为了简单。
logisticRegr.score(test_img, test_lbl)
主成分分析后拟合逻辑回归的时间
本节教程的全部目的是向你展示可以使用PCA来加速机器学习算法的拟合。下表显示了在我的MacBook上使用PCA(每次保留不同数量的方差)后进行logistic回归所花费的时间)。
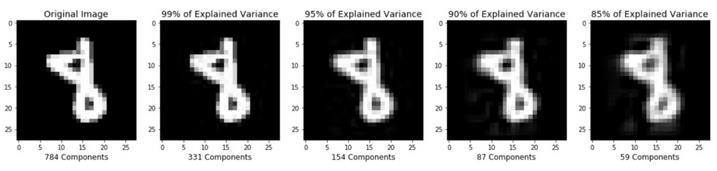
压缩后的图像重建
本教程前面的部分演示了如何使用PCA将高维数据压缩为低维数据。我想简要地提一下,PCA还可以将数据的压缩重建(低维数据)还原为原始高维数据的近似形式。如果你对生成下图的代码感兴趣,请查看我的github(https://github.com/mGalarnyk/Python_Tutorials/blob/master/Sklearn/PCA/PCA_Image_Reconstruction_and_such.ipynb)。
总结思想
这篇文章我本来可以写得更长一些,因为PCA有很多不同的用途。我希望这篇文章能对你有所帮助。我的下一个机器学习教程将介绍如何理解用于分类的决策树(https://towardsdatascience.com/understanding-decision-trees-for-classification-python-9663d683c952)。
原文作者:Michael Galarnyk
翻译作者:Sophie Li
美工编辑:过儿
校对审稿:Dongdong
原文链接:https://towardsdatascience.com/pca-using-python-scikit-learn-e653f8989e60





