
使用 PySpark 和 MLlib 构建线性回归预测波士顿房价
Apache Spark已经成为机器学习和数据科学中最常用和受支持的开源工具之一。
在这篇文章中,我将帮助您开始使用Apache Spark的Spark.ml的线性回归预测波士顿房价。我们的数据来自Kaggle比赛:波士顿郊区的住房价值。对于每一个观测,我们有以下资料:
CRIM — 城镇的人均犯罪率。
ZN — 土地面积超过25000平方英尺的住宅用地所占比例。
INDUS — 每个城镇非零售商业面积的比例。
CHAS — 查尔斯河虚拟变量(土地河流交界= 1;否则=0)。
NOX — 氮氧化物浓度(千万分之一)。
RM — 每个住宅的平均房间数。
AGE — 1940年以前建造的自住房屋的比例。
DIS — 到波士顿五个就业中心距离的加权平均值。
RAD — 放射状公路的可达性指数。
TAX — 全价值的房产税率(每1万美元)。
PTRATIO — 城镇的学生与教师比例。
BLACK — 1000(Bk — 0.63)² , Bk为各城镇黑人所占比例。
LSTAT — 人口中较低地位(百分比)。
MV — 业主自住房屋的中值(1000美元)。这是目标变量。
输入数据集包含了各个房屋的详细信息。根据所提供的信息,目标是拟出一个模型来预测该地区某所房子的中值。
加载数据
from pyspark import SparkConf, SparkContextfrom pyspark.sql import SQLContextsc= SparkContext()sqlContext = SQLContext(sc)house_df = sqlContext.read.format('com.databricks.spark.csv').options(header='true', inferschema='true').load('boston.csv')house_df.take(1)[Row(CRIM=0.00632, ZN=18.0, INDUS=2.309999943, CHAS=0, NOX=0.537999988, RM=6.574999809, AGE=65.19999695, DIS=4.090000153, RAD=1, TAX=296, PT=15.30000019, B=396.8999939, LSTAT=4.980000019, MV=24.0)]
数据探索
以树状格式打印schema。
house_df.cache()house_df.printSchema()root|-- CRIM: double (nullable = true)|-- ZN: double (nullable = true)|-- INDUS: double (nullable = true)|-- CHAS: integer (nullable = true)|-- NOX: double (nullable = true)|-- RM: double (nullable = true)|-- AGE: double (nullable = true)|-- DIS: double (nullable = true)|-- RAD: integer (nullable = true)|-- TAX: integer (nullable = true)|-- PT: double (nullable = true)|-- B: double (nullable = true)|-- LSTAT: double (nullable = true)|-- MV: double (nullable = true)
进行描述性分析
house_df.describe().toPandas().transpose()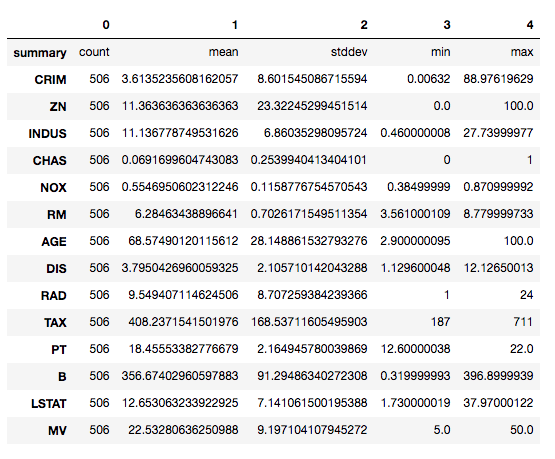
散点矩阵是粗略判断多个自变量之间是否存在线性相关的好方法。
import pandas as pdnumeric_features = [t[0] for t in house_df.dtypes if t[1] == 'int' or t[1] == 'double']sampled_data = house_df.select(numeric_features).sample(False, 0.8).toPandas()axs = pd.scatter_matrix(sampled_data, figsize=(10, 10))n = len(sampled_data.columns)for i in range(n):v = axs[i, 0]v.yaxis.label.set_rotation(0) v.yaxis.label.set_ha('right') v.set_yticks(()) h = axs[n-1, i] h.xaxis.label.set_rotation(90) h.set_xticks(())
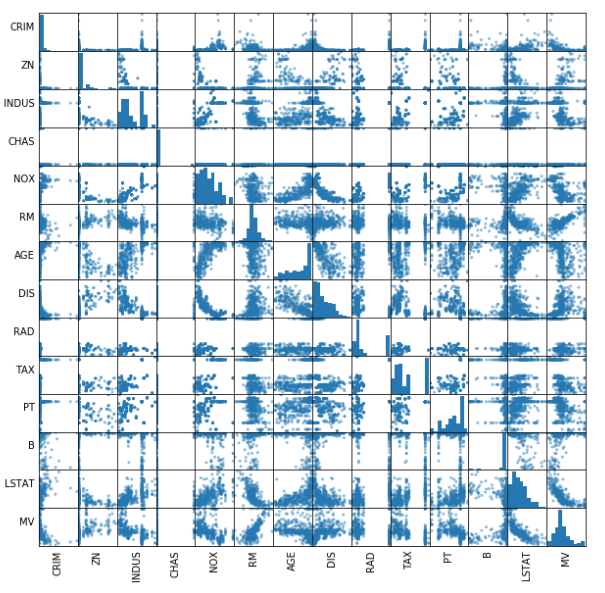
这样很难看清楚。那让我们找出自变量和目标变量之间的相关性。
import sixfor i in house_df.columns:if not( isinstance(house_df.select(i).take(1)[0][0], six.string_types)):print( "Correlation to MV for ", i, house_df.stat.corr('MV',i))Correlation to MV for CRIM -0.3883046116575088Correlation to MV for ZN 0.36044534463752903Correlation to MV for INDUS -0.48372517128143383Correlation to MV for CHAS 0.17526017775291847Correlation to MV for NOX -0.4273207763683772Correlation to MV for RM 0.695359937127267Correlation to MV for AGE -0.37695456714288667Correlation to MV for DIS 0.24992873873512172Correlation to MV for RAD -0.3816262315669168Correlation to MV for TAX -0.46853593528654536Correlation to MV for PT -0.5077867038116085Correlation to MV for B 0.3334608226834164Correlation to MV for LSTAT -0.7376627294671615Correlation to MV for MV 1.0
相关系数的范围是从-1到1。当接近1时,表示存在强的正相关关系。例如,当房间数量增加时,中值就会增加。当系数接近-1时,说明存在较强的负相关关系;当人口中地位较低的百分比上升时,中值趋于下降。最后,系数接近于零意味着不存在线性相关。
目前,我们要保留所有的变量。
为机器学习准备数据。我们只需要两栏-特征和标签(“MV”):
from pyspark.ml.feature import VectorAssemblervectorAssembler = VectorAssembler(inputCols = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PT', 'B', 'LSTAT'], outputCol = 'features')vhouse_df = vectorAssembler.transform(house_df)vhouse_df = vhouse_df.select(['features', 'MV'])vhouse_df.show(3)
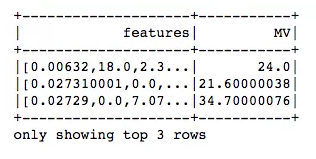
Figure 3splits = vhouse_df.randomSplit([0.7, 0.3])train_df = splits[0]test_df = splits[1]线性回归
from pyspark.ml.regression importLinearRegressionlr = LinearRegression(featuresCol = 'features', labelCol='MV', maxIter=10, regParam=0.3, elasticNetParam=0.8)lr_model = lr.fit(train_df)print("Coefficients: " + str(lr_model.coefficients))print("Intercept: " + str(lr_model.intercept))Coefficients: [0.0,0.007302310571175137,-0.03286303124593804,1.4134773328268,-7.91932366863737,5.341921692409693,0.0,-0.5791187396097941,0.0,-0.0010503197747184644,-0.7748333592630333,0.01126108224671488,-0.3932170620689197]Intercept: 11.327590788070061
总结训练集上的模型,并打印出一些指标:
trainingSummary = lr_model.summaryprint("RMSE: %f" % trainingSummary.rootMeanSquaredError)print("r2: %f" % trainingSummary.r2)RMSE: 4.675914r2: 0.743627
RMSE测量模型的预测值与实际值之间的差异。然而,只有当我们与实际的“MV”值(如平均值、最小值和最大值)进行比较时,RMSE才是没有意义的。经过这样的比较,我们的RMSE看起来相当不错。
train_df.describe().show()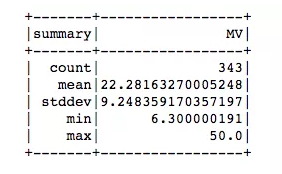
R squared 为0.74表明,在我们的模型中,“MV”的可变性约有74%可以用该模型加以解释。这与scikiti – learn的结果一致。还不错。但是,我们必须注意,训练集上的性能可能与测试集上的性能不是很接近。
lr_predictions = lr_model.transform(test_df)lr_predictions.select("prediction","MV","features").show(5)from pyspark.ml.evaluation import RegressionEvaluatorlr_evaluator = RegressionEvaluator(predictionCol="prediction", \labelCol="MV",metricName="r2")print("R Squared (R2) on test data = %g" % lr_evaluator.evaluate(lr_predictions))
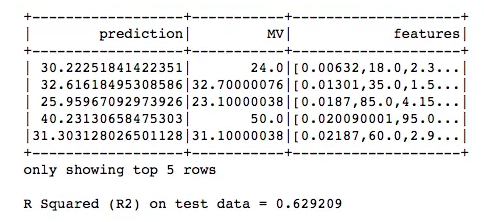
test_result = lr_model.evaluate(test_df)print("Root Mean Squared Error (RMSE) on test data = %g" % test_result.rootMeanSquaredError)
测试数据集的均方根误差(RMSE) = 5.52048
毫无疑问,我们在测试集中得到了更差的RMSE和R squared。
print("numIterations: %d" % trainingSummary.totalIterations)print("objectiveHistory: %s" % str(trainingSummary.objectiveHistory))trainingSummary.residuals.show()numIterations: 11objectiveHistory: [0.49999999999999956, 0.4281126976069304, 0.22539203628598917, 0.20185326295592582, 0.1686847843494657, 0.16588096079648484, 0.16543041085178495, 0.16508485781434112, 0.16484472289473545, 0.16454785266359198, 0.16447743850144508]

用我们的线性回归模型做一些预测:
predictions = lr_model.transform(test_df)predictions.select("prediction","MV","features").show()
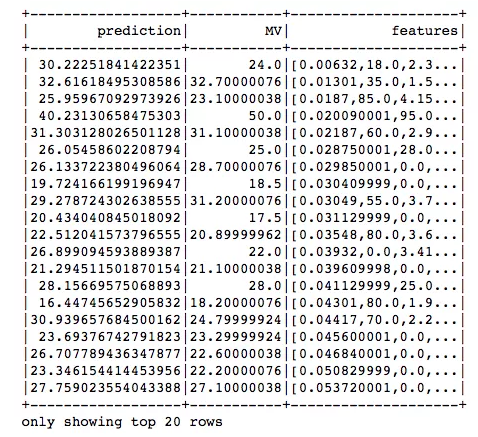
决策树回归
from pyspark.ml.regression import DecisionTreeRegressordt = DecisionTreeRegressor(featuresCol ='features', labelCol = 'MV')dt_model = dt.fit(train_df)dt_predictions = dt_model.transform(test_df)dt_evaluator = RegressionEvaluator(labelCol="MV", predictionCol="prediction", metricName="rmse")rmse = dt_evaluator.evaluate(dt_predictions)print("Root Mean Squared Error (RMSE) on test data = %g" % rmse)
测试数据上的RMSE = 4.39053
特征重要度
t_model.featureImportancesSparseVector(13, {0: 0.0496, 1: 0.0, 4: 0.0118, 5: 0.624, 6: 0.0005, 7: 0.1167, 8: 0.0044, 10: 0.013, 12: 0.1799})house_df.take(1)[Row(CRIM=0.00632, ZN=18.0, INDUS=2.309999943, CHAS=0, NOX=0.537999988, RM=6.574999809, AGE=65.19999695, DIS=4.090000153, RAD=1, TAX=296, PT=15.30000019, B=396.8999939, LSTAT=4.980000019, MV=24.0)]
显然,在我们的数据中,房间数量是预测房价中位数最重要的特征。
梯度回归树(GBDT)
from pyspark.ml.regression import GBTRegressorgbt = GBTRegressor(featuresCol = 'features', labelCol = 'MV', maxIter=10)gbt_model = gbt.fit(train_df)gbt_predictions = gbt_model.transform(test_df)gbt_predictions.select('prediction', 'MV', 'features').show(5)
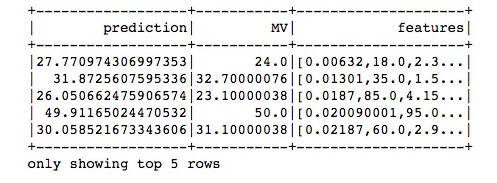
gbt_evaluator = RegressionEvaluator( labelCol="MV", predictionCol="prediction", metricName="rmse")rmse = gbt_evaluator.evaluate(gbt_predictions)print("Root Mean Squared Error (RMSE) on test data = %g" % rmse)测试数据上的RMSE = 4.19795
梯度回归树在我们的数据上表现最好。
源代码可以在Github上找到。我很高兴听到任何反馈或问题。
原文作者:Susan Li
翻译作者:Sophie Li
美工编辑:过儿
校对审稿:Dongdong
原文链接:https://towardsdatascience.com/building-a-linear-regression-with-pyspark-and-mllib-d065c3ba246a





