
如何在分类算法中使用逻辑回归
监督学习算法对目标预测输出和输入特征之间的关系进行建模,这样,我们可以根据先前数据集中学到的那些关系来预测新数据的输出值。监督学习算法(Supervised learning algorithms)可以分为以下两大类:
- 回归(Regression):预测连续的目标变量。例如,预测房价就是回归任务的一种 。
- 分类(Classification):预测离散的目标变量。例如,预测电子邮件是否为垃圾邮件,就是分类任务的一种。
本文将带你了解逻辑回归和相关的概率知识。如果你想了解更多数据分析相关内容,可以阅读以下这些文章:
DS数据科学家和DA数据分析师:要学习什么不同内容?
数据分析师需要知道的10个Excel函数
数字营销是怎样通过数据分析赚钱的?
数据分析如何在Fintech中发挥作用?
逻辑回归(Logistic Regression)是一种监督学习算法,尽管它包含“回归”这个词,但主要用于解决二元“分类”任务。“回归”与“分类”相矛盾,但逻辑回归的重点其实是在“逻辑”这个词,它指的是逻辑函数,在算法中实际上用于完成分类任务。
逻辑回归是一种简单而有效的分类算法,因此常用于二元分类任务。客户流失、垃圾邮件、网站或广告点击预测是逻辑回归提供有效解决方案的示例,甚至用作神经网络层的激活函数。
逻辑回归的基础是逻辑函数,也称为S型函数(Sigmoid Function),取实数值并将其映射至 0 到 1 之间的值。
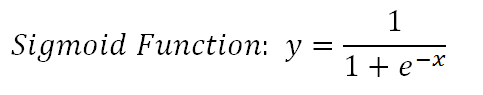
逻辑回归模型以线性方程为输入值,使用逻辑函数和对数几率,执行二元分类任务。在详细介绍逻辑回归之前,我们先回顾一下概率(Probability)范围内的一些概念。
# 概率(Probability) #
概率(Probability)衡量事件发生的可能性。例如,我们说“垃圾邮件的概率为90%”:
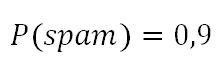
几率(Odds)是正类(垃圾邮件)和负类(非垃圾邮件)的概率之比。
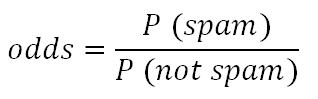
对数几率(Log Odds)是几率的对数。
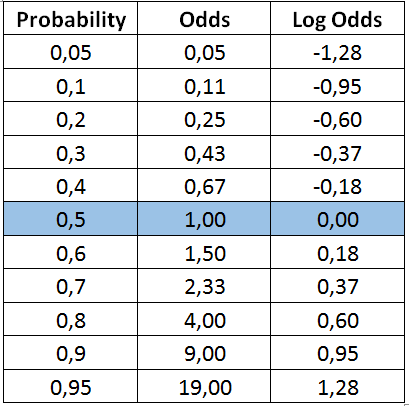
以上概念,本质上都代表相同的衡量标准,但采取的方式不同。如果采用逻辑回归,我们就会使用对数几率(Log Odds)。这也就是在逻辑回归算法中首选对数几率的原因。
对数几率是几率的对数,几率是正类与负类的概率之比。
概率为0.5,意味着垃圾邮件与非垃圾邮件的可能性相同。这里可以注意一下,概率为 0.5 的对数几率是 0。我们会用到这一点。
让我们回到 S型函数,通过不同的等式表示:
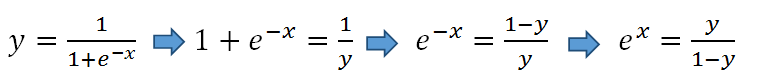
等式两边都取自然对数:
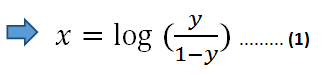
在等式 (1) 中,我们可以使用线性方程 z 代替 x:
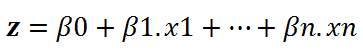
那么等式(1)表示为:
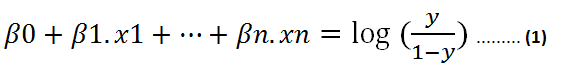
假设 y 是正类的概率。如果 z 为 0,则 y 为 0.5。对于 z 的正值,y 大于 0.5,对于 z 的负值,y 小于 0.5。如果正类的概率大于 0.5(即概率大于50%),我们可以将结果预测为正类 (1)。反之结果为负类 (0)。
注意:在二元分类中,表示两种分类结果的方法很多,例如Positive/Negative,1/0,True/False。
下表是一些z值及其对应的y(概率)值。所有实数都映射在 0 和 1 之间。
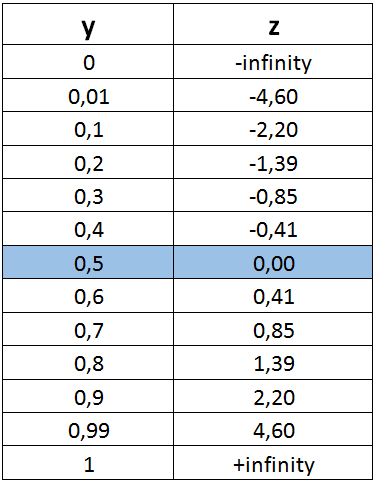
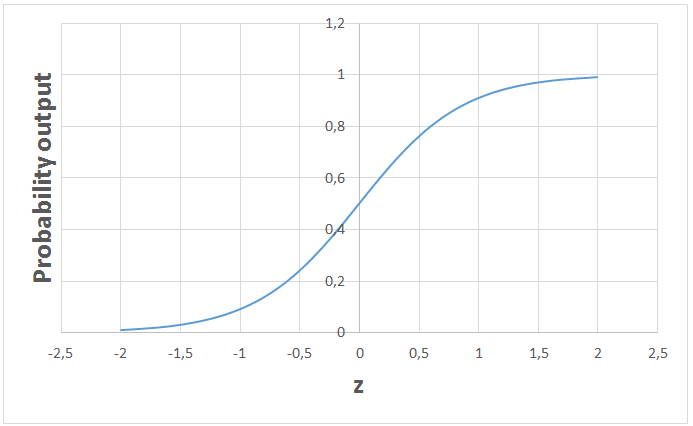
如果我们把这个函数绘制出来,将得到著名的逻辑回归 s 形图:
分类问题归最终可以总结为一个线性方程:
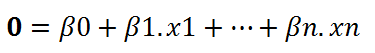
这看起来就像是在解决线性回归问题。在训练阶段,我们用极大似然估计法(maximum-likelihood estimation algorithm)确定函数参数。然后,对于给定的自变量 (x1, … xn) 值,我们就可以得出正类的概率。
我们可以直接使用计算的概率结果。例如,输出值可以是垃圾邮件的概率为 95%,或者客户点击此广告的概率为 70%。但是,在大多数情况下,概率会被用于对数据点进行分类。比如,如果概率大于 50%,则预测为正类 (1)。否则,预测为负类 (0)。而且,我们只是将线性回归问题的解决方案转换为二元分类任务。
逻辑回归是一种简单却有效的算法,用于解决二元分类问题。逻辑函数(即 S型函数)也经常作为输出层的激活函数,用于复杂的神经网络中。
感谢你的阅读。如果有任何反感谢你的阅读。如果有任何反馈,可随时在下方评论。你还可以订阅我们的YouTube频道,观看大量数据科学相关公开课:https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ;在LinkedIn上关注我们,扩展你的人际网络!https://www.linkedin.com/company/dataapplab/
原文作者:Soner Yildirim
翻译作者:Lia
美工编辑:过儿
校对审稿:Jiawei Tong
原文链接:https://towardsdatascience.com/how-is-logistic-regression-used-as-a-classification-algorithm-51eaf0d01a78





