
如何理解机器学习中的Bias & Variance?
找到偏差和方差的平衡点是成功的诀窍。
在预测分析中,我们建立模型来预测全新的、从未见过的样本。整个过程的目的是为了去预测未知事件。但模型不可能直接一下子就给出预测。我们要用样本训练模型,然后期望模型能就那些具有相同分布的新样本进行预测。
世上没有完美的模型,我们建立与训练的模型总是有错误的。预测结果和真实值总会有差异。模型性能则与这个差值呈反相关,差异越小,模型越好。我们的目标就是尽量让误差最小化,我们不可能消除误差,但可以让它降低。而误差中可以被降低的部分由两项构成:偏差和方差。
模型性能取决于偏差和方差的平衡,最优模型就位于二者中间的某个位置。要注意,在偏差和方差之间总是存在着权衡。我们的挑战便是要找到正确的平衡。
偏差和方差是什么?
偏差出现于我们用简化模型去近似复杂关系的时候。例如一组自变量和因变量的关系十分复杂,是非线性的,但我们却试图采用线性回归模型。这样的话,就算有千百万的训练样本,我们也建立不了一个准确的模型。采用简化模型时,我们便自动限制了模型的性能,因为模型无法反应特征和目标变量之间的真实关系。
偏差较高的模型抓不住关键重要的关系。因此,训练和验证集的准确率都会较低。这种情况又叫欠拟合。偏差高的模型易于欠拟合。以下面的散点图为例,其展示了一个特征变量和目标变量的关系。如果我们用红线做模型来预测蓝点所描述的关系,那模型的偏差就太高了,对数据是欠拟合的。
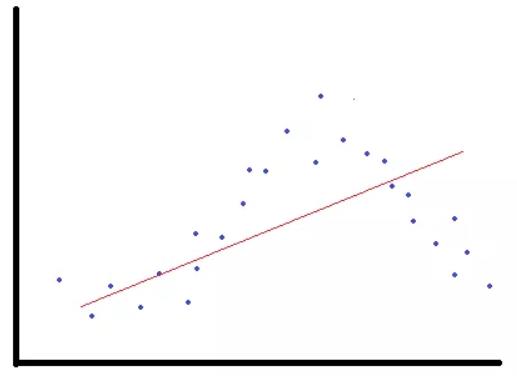
方差出现于模型对自变量的变化高度敏感的时候。模型试图提取特征和目标关系中的一切细节,甚至会学习数据中可能随机出现的噪声。而一个特征变量很小的变动就可能改变整个模型的预测结果。因此,我们的模型会抓住训练集内的所有细节,训练集的准确率就会非常高。然而,一个全新、从未见过的样本的准确率就不会太好了,因为特征变量总会有各种不同的变化。这种情况又叫过拟合。模型对训练集过拟合,但对数据集里的真实关系却不能很好地泛化。模型在那些见过的样本上的准确率会很高但在新样本上的准确率则会较低。用上述同样的例子,如果我们用下图红色曲线来模拟该关系,模型就过拟合了。可以看到,它高度敏感,且试图抓取所有的变化。
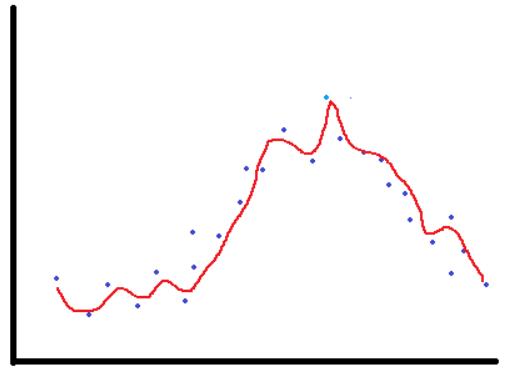
所以高偏差和高方差都不好。完美的模型要有低偏差和低方差。然而,就算有可能,要找到完美的模型也十分困难。偏差和方差之间总是存在权衡。我们的目标应该是去找到二者间的正确平衡,这是机器学习工程师成功的诀窍。而在我们的例子里,一个合适的模型应该是类似这样的:
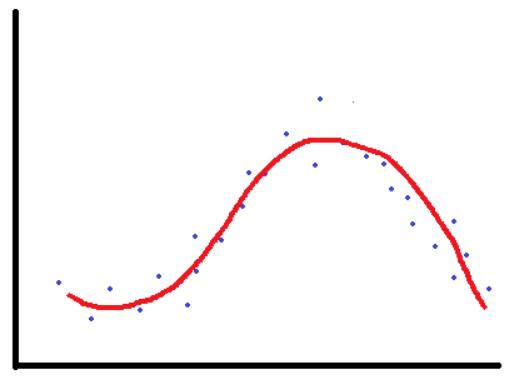
感谢阅读~
原文作者:Soner Yildirim
翻译作者:Siyu Hao
美工编辑:过儿
校对审稿:Dongdong
原文链接:https://towardsdatascience.com/bias-and-variance-in-machine-learning-b8019a5a15bc





