带你了解什么是Covariance Matrix协方差矩阵

线性代数（Linear Algebra）是机器学习的基础之一，被认为是“数据中的数学知识”。虽然我个人非常喜欢线性代数中的大多数知识，但有些概念在一开始会很难掌握。我很难以想象要如何将其中一些概念运用到现实中的应用，或某些概念能产生的实际效益。

然而，协方差矩阵（Covariance Matrix）改变了这种现况。

协方差和相关性的概念体现了线性代数中的某些知识。像PCA这样的算法，很大程度上依赖于协方差矩阵的运算，而协方差矩阵在获取主要成分起着重要的作用。

接下来，我们将学习什么是协方差矩阵，如何运算协方差矩阵及其具体操作。但首先，我们需要了解相关概念和基础知识，从而更深层次地了解协方差矩阵。如果你想了解更多数据分析相关内容，可以阅读以下这些文章：
数据分析师需要知道的10个Excel函数
新兴报表工具FineReport——商业分析师需要知道的三种报表
数字营销是怎样通过数据分析赚钱的？
三个必备高级分析方法，了解你的客户

什么是相关性（Correlation），相关性有什么用？

相关性分析（Correlation Analysis）旨在确定变量之间的共性。

假设，我们随机抽取一群人，并测量两个变量—“身高”和“体重”。一般情况下，我们预想中的情况是：高的人比矮的人重。这类关系的散点图如下所示：

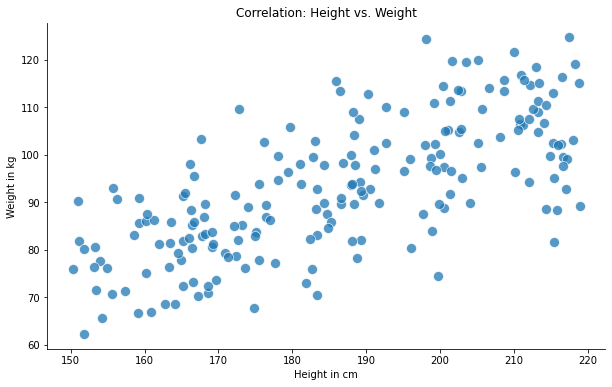
身高和体重散点图 [图片由作者提供]

通过查看该散点图，我们可以清楚地看出两个变量是相关的。相关性，或者更具体地说是相关系数，为我们提供了一种统计度量，从而量化这种关系。

系数范围从-1到+1，具体如下：

• 1. 正相关 – 即两个变量朝同一方向移动，例如两个值同时增加。 
• 2. 负相关——描述负相关的变量。即如果一个变量增加，另一个变量减少，反之亦然。
• 3. 相关系数为0，表明两个变量之间不存在任何关系。

注意：相关系数仅限于线性，因此不会量化任何非线性关系。如果测量非线性关系，可以使用其他方法，例如互信息法或转换变量。

那我们为什么还要考虑相关性呢？

事实证明，相关系数和协方差这两个概念基本上没有什么区别，因此密切相关。相关系数只是协方差绑定到范围[-1,1]的标准化版本。

这两个概念都依赖于同一基础概念：方差和标准差。

引入方差（Variance）和标准差（Standard Deviation）

方差作为分散的度量，可用于表明数据值的差异或分布情况。

我们可以通过取每个数据值与均值的差的平均值，从而计算方差，也就是每个数据点到中心的差距。

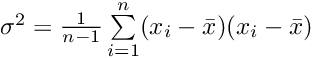
通过查看上述等式，我们可以知道，当所有数据值都接近均值时，方差会较小；如果数据点离中心较远，方差会较大。

我们可以具体通过以下两个实例了解详情：

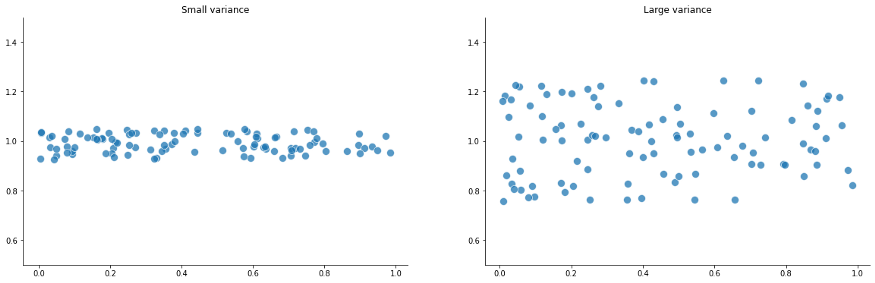
我们了解了方差，也就了解了标准差，它是方差的平方根。

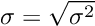
现在，我们已经了解了基本概念，下一节中，我们可以将这些概念联系在一起。

协方差（Covariance）和协方差矩阵（Covariance Matrix）

假设我们有一个具有两个特征的数据集，我们想要描述数据中的不同关系。协方差的概念可以为我们提供工具，从而测量两个变量之间的方差。

我们可以稍微修改之前的等式，从而计算协方差，基本上得出两个变量之间的方差。

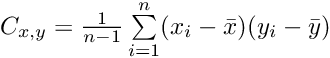
如果我们对之前对数据进行均值中心化处理，则可以将等式简化为：

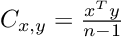
简化后，我们可以看到，协方差的计算其实很简单，即两个包含数据的向量的点积。

假设有一个数据集，包含三个特征，分别为 x、y 和 z。计算协方差矩阵将产生一个 3 x 3 的矩阵。该矩阵包含每个特征与所有其他特征及其本身的协方差。我们可以将协方差矩阵想象成：

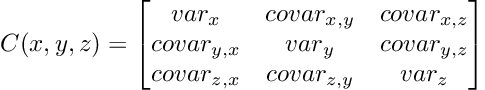
协方差矩阵是对称，且逐个按特征成形的。对角线包含单个特征的方差，而非对角线包含协方差。

我们已经知道如何计算协方差矩阵，现在，我们只需要将上述等式中的向量与以均值为中心的数据矩阵交换。

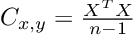
得出结果后，我们就可以用之前学习相关系数时所描述的方法来解释协方差矩阵。

运用所学知识

现在我们已经完成了基础工作，可以开始运用所学知识了。

出于测试目的，我们将使用鸢尾花卉（iris）数据集。数据集由 150 个样本组成，具有 4 个不同特征（萼片长度、萼片宽度、花瓣长度、花瓣宽度）

我们通过在散点图中绘制前两个特征，从而初步了解数据。

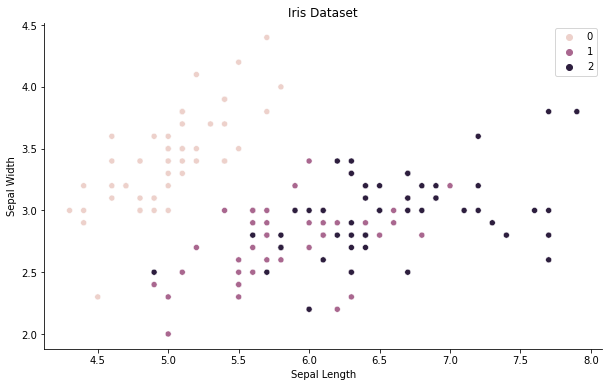
通过绘制前两个特征概述iris 数据集 [图片由作者提供]

我们的目标是“手动”计算协方差矩阵。因此，在此之前，我们需要先对数据进行均值中心化处理。为此，我们确定并应用以下函数：

def standardize_data(X):
    numerator = X - np.mean(X, axis=0)
    denominator = np.std(X, axis=0)
    return numerator / denominator

X_scl = standardize_data(X)

print('Mean:', np.mean(X_scl))
print('Std:', np.std(X_scl))

注意：我们会通过减去平均值，并将其除以标准差，从而对数据进行标准化处理。

通过运行上图中的代码，标准化处理数据，结果为：平均值为0，标准偏差为1。

接下来，我们可以计算协方差矩阵。

def get_covariance_matrix(X, ddof=0):
    n_samples = X.shape[0]
    C = np.dot(X.T, X) / (n_samples - ddof)
    return C

C = get_covariance_matrix(X_scl, ddof=0)

print(C.shape)

注意：使用 NumPy 的内置函数 numpy.cov(x) 同样可以实现相同计算。

我们的协方差矩阵是一个 4 x 4 的矩阵，逐个按特征成形。我们可视化矩阵和协方差，具体如下图：

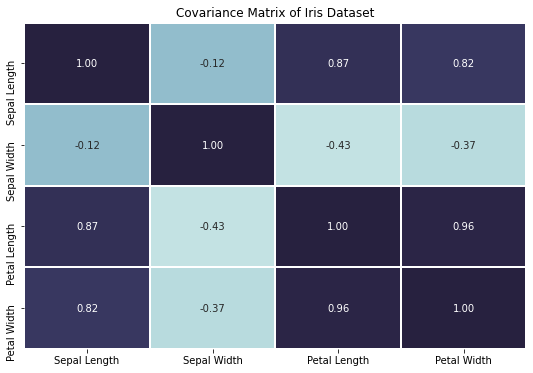
通过获得高协方差或相关系数，我们可以清楚地看到不同特征之间的许多相关性。例如，花瓣长度看起来是与花瓣宽度高度呈正相关的，按常识讲也是这样——长的花瓣可能更宽。

结论

在本文中，我们学习了如何计算和展示协方差矩阵。我们还介绍了一些相关概念，例如方差、标准差、协方差和相关性。

协方差矩阵在主成分分析中起着核心作用。通过手动实现或计算，可以将许多重要的部分联系在一起，并为线性代数概念注入活力。

感谢您的阅读！你还可以订阅我们的YouTube频道，观看大量数据科学相关公开课：https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ；在LinkedIn上关注我们，扩展你的人际网络！https://www.linkedin.com/company/dataapplab/

原文作者：Marvin Lanhenke
翻译作者：Lia
美工编辑：过儿
校对审稿：Jiawei Tong
原文链接：https://towardsdatascience.com/understanding-the-covariance-matrix-92076554ea44