不可不知的数据科学基础 ——AB Testing

我们将用一个简单的例子来探索A/B测试的投入和产出 (也可称为, 假设检验)。

因此，在接下来的文章里，我将逐一介绍每个数据科学家和有抱负的数据科学家(像我一样)都应该拥有的核心工具，以便我们都能在面试中取得好成绩!现在进入今天的话题！

伪装的假设检验

如果你有统计学背景，你可能会想，A/B测试和假设检验是一样的吗？没错，是的！让我们通过一个简单的例子来探讨假设检验是如何工作的来证明A/B检验。

想象一下，我们的客户，一个非常成功的个人理财app的所有者，带着以下问题来找我们：

“托尼，我们重新设计的新应用程序是为了帮助人们节省更多的钱。但这真的有效吗?请帮助我们解决这个问题，以便我们决定是否部署它。”

所以我们的工作是确定人们是否会因为新的应用程序设计而节省更多的钱。首先，我们需要确定我们是否有所需的所有数据。我们会问:“你已经收集了哪些可能有用的数据？”

原来我们的客户已经做了一个实验并收集了一些数据：

• 6个月前，我们的客户随机选择了1000名新注册的用户，其中500人作为对照组，500人作为实验组。
• 对照组继续使用当前的应用程序。
• 与此同时，试验组被暴露在重新设计的应用程序中。所有用户一开始的储蓄率都是0%。
• 这1000名用户只占该应用总用户的一小部分。

六个月后，我们的客户记录了实验中所有1000个用户的储蓄率。储蓄利率是每个用户每月储蓄占工资的百分比。她得出了以下的结论：

对照组的平均储蓄率从0%上升到12%，标准差为5%。

实验组的平均储蓄率从0%上升到13%，标准差为5%。

我们的实验结果如下图所示:

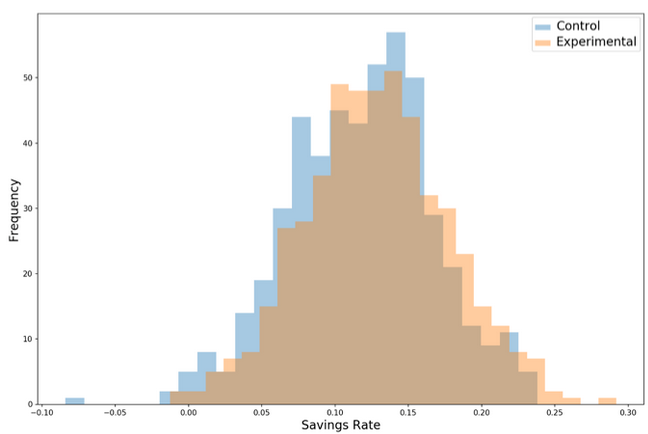
对照组与试验组的存储率的对比直方图

六个月后，实验组的成员看起来确实比对照组的成员有更高的储蓄率。那么，仅仅画出这个柱状图，展示给我们的客户，就足够了吗?

不！因为我们仍然不能确定我们观察到的储蓄增长是真实的。幸运的是，在我们的实验中，我们可以以这样一种方式抽取用户，即那些希望存更多钱的人最终都进入了试验组。为此，我们要提出以下问题：

我们得到随机观察结果的可能性有多大?

回答这个问题是假设检验(和A/B检验)的关键。

零假设 (Null Hypothesis)

想象一下，在现实中，新的应用程序设计并不能帮助用户节省更多的钱。然而，即使新的设计是无用的，当我们进行实验时，仍然有可能观察到储蓄率的增加。

怎么会这样呢?因为我们进行了抽样。例如，如果我从成千上万的人群中随机挑选100个人并计算他们的平均身高，我可能得到5英尺8英寸。如果我再做几次，下一次我可能会得到5英尺10英寸，下一次是5英尺7英寸。

因为计算统计量时使用的是样本而不是总体，所以计算的每个样本均值都是不同的。

知道了抽样会引起变化，我们可以将上面的问题重新定义为：

如果新的应用程序设计对人们的储蓄的影响真的是零，那么从随机机会中观察到储蓄增长如此之大的概率是多少?

可以说，我们的零假设是——对照组的储蓄率增长等于实验组的储蓄率增长。

我们现在的工作是测试零假设。我们可以通过概率思维实验来做到这一点。

反复模拟实验

想象一下，我们可以很容易地、立即地一次又一次地运行我们的实验。此外，我们仍然处在一个并行的世界，在那里新的应用程序设计是无用的，对用户的节省没有任何效果。我们会观察到什么?

对于这个问题，我们是这样模拟的：

• 取两个与对照组统计特征相同的正态分布随机变量(均值= 12%，标准差= 5%)各抽取500次(对照组有500个用户，实验组有500个用户)。这些将是我们的控制组和试验组(相同的意思是因为我们的新设计没有任何效果)。在这里使用泊松分布的随机变量在技术上更正确，但是为了简单起见，我们使用正态分布的随机变量。
• 记录两组间的平均储蓄率差异(即用实验组的平均储蓄率减去对照组的平均储蓄率)。
• 重复以上步骤10000次。
• 画一个柱状图来表示两组之间平均节约量的差异。

当我们这样做时，我们得到下面的直方图。柱状图显示了由于随机机会(由随机抽样组成)，组与组之间的平均储蓄率差异有多大。

红色的竖线显示了我们在客户进行实验时实际观察到的平均储蓄率差异(1%)的百分比，观察右边的红线在下面的柱状图是我们价值的概率——观察节省大量增加1%从随机的机会(我们这里只做了一个单边测试，因为它更容易理解和想象)。

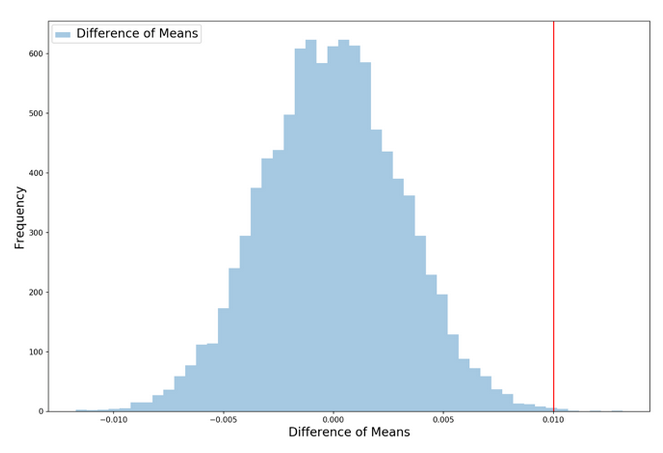
在这种情况下，这个值非常低——在我们进行的10000次实验中，只有9次(假设新设计对节省的影响为零)，我们观察到组均值的差异为1%或更大。

这意味着，由于随机的机会，观察到一个像我们这样高的值只有0.09%的变化！

0.09%的概率是p值。关于假设检验(和A/B检验)确实有很多统计术语，我们将把大部分留给维基百科来解释。

我们的目标，一如既往，是建立一个对这些工具如何和为什么工作的直观理解——所以一般来说，我们将避免使用术语，而倾向于尽可能简单的解释。然而，p值是一个非常重要的概念，你会在数据科学世界中遇到很多，所以我们必须面对它。p值(我们在上面的模拟中计算出的0.09%)表示：

零假设成立时观测到的东西的概率。

因此，p值就是我们用来检验零假设是否正确的数字。根据它的指示，看起来我们想要一个尽可能低的p值，p值越低，我们在实验中运气好的可能性就越小。在实践中，我们将设置一个p- value cutoff (称为alpha)，低于这个值，我们将拒绝原假设，并得出观察到的效果/影响最有可能是真实的(统计意义)的结论。

现在让我们探索一个统计性质，使得我们可以快速计算p值。

中心极限定理

现在是讨论统计学的一个基本概念—-中心极限定理—-的好时机，如果你把独立随机变量相加，它们的标准化和会趋于正态分布。当你把越来越多的随机变量相加时。即使随机变量本身不是来自正态分布，中心极限定理也成立。

换而言之-如果我们计算一组样本均值(假设我们的观察是相互独立的，就像硬币的Aips是独立的)，所有这些样本均值的分布将是正态分布。

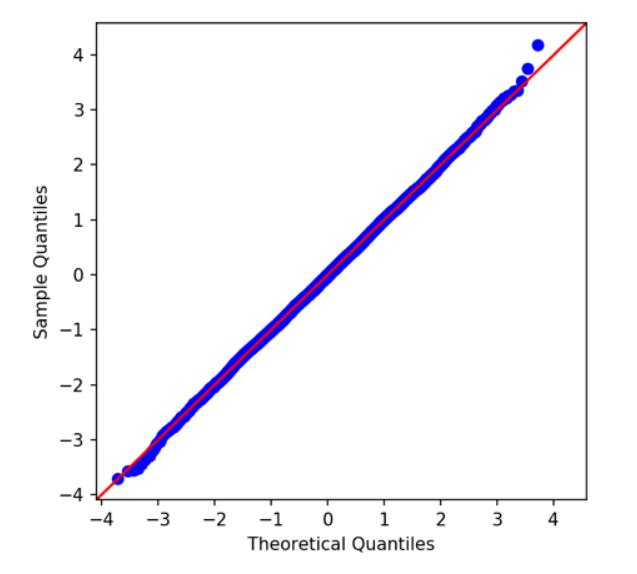
看一下我们之前计算的平均值差异的直方图。看起来像正态分布，对吧？我们可以使用Q- Q图来验证正态性，该图将我们的分布分位数与参考分布(在本例中为正态分布)的分位数进行比较。如果我们的分布是正态的，它会紧靠红色的45度线。的确如此，酷!

当我们不断地进行储蓄实验时，这就是中心极限定理的实际应用！

为什么这很重要呢?

还记得我们之前是如何通过运行10,000次实验来测试零假设的吗？听起来是不是很累？实际上，重复进行实验既累人又昂贵。但多亏了中心极限定理，我们不需要！

我们知道我们的重复实验的分布会是什么样子—-正态分布,我们可以使用这些知识来统计推断的分布10000实验没有实际运行他们！

让我们回顾一下目前已知的情况：

• 我们观察到对照组和实验组之间的平均储蓄率差异为1%。我们想知道这是真实的差异还是统计上的干扰。
• 我们知道我们需要对实验结果半信半疑，因为我们只对客户用户总数中的一小部分样本进行了实验。如果我们在新的样本上再做一次，结果会发生变化。
• 由于我们担心在现实中新的app设计对储蓄没有影响，我们的零假设是对照组和实验组之间的均值差异为零。
• 由中心极限定理可知，如果我们重复抽样并进行新的实验，这些实验的结果(对照组和实验组之间观察到的平均差异)将呈正态分布。
• 由统计可知，取两个独立随机变量的差异时，结果的方差等于各个体方差之和：

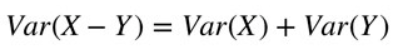
完成这个目标

好了！现在我们有了运行假设检验所需的所有东西。所以让我们继续完成我们从客户那里收到的任务：

• 首先，在观察数据产生偏差之前，我们需要选择一个阀值, 也被称为alpha (如果计算出的p值小于alpha，我们拒绝零假设，并得出新的设计增加了储蓄率的结论)。alpha值对应于我们产生假阳性的概率——拒绝实际上是正确的零假设。0.05在统计学中是很标准的所以我们就用它。
• 接下来，我们需要计算测试统计量。测试统计量是上述直方图的数值等价，它告诉我们，观察值(1%)离原假设值(在本例中为零)有多少个标准差远。我们可以这样计算:

• 标准误(standard error)为实验组的平均储蓄率与对照组的平均储蓄率之差的标准差。在上面的图中，标准误由蓝色直方图的宽度表示。回想一下，两个随机变量的差异的方差等于个体方差的和(而标准差是方差的平方根)。我们可以很容易地计算出标准误差使用信息，我们已经有:

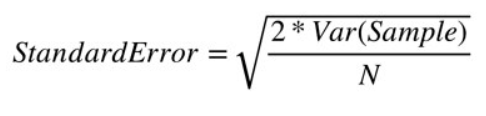
• 记住，对照组和实验组的储蓄率的标准差都是5%。样本方差是0.0025而N是每组的观测值所以N = 500。把这些数代入公式，标准误差是0.316%
• 在检验统计量公式中，观察值为1%，假设值为0%(因为我们的零假设是不存在差异的)。把这些值和刚刚计算的标准误差一起代入检验统计量公式，我们得到的检验统计量是0.01/0.00316 = 3.16。
• 观察值为1%，离假设值0%有3.16个标准差远。这太多了。我们可以使用下面的Python代码来计算p值(用于双边测试)。p值是0.0016。请注意，我们在双边检验中使用p值，因为我们不能自动假设新的设计与当前的设计相同或更好——新的设计也可能更差，而双边检验解释了这种可能性。

from scipy.stats import norm
# Two Tailed Testprint('The p-value is: ' + str(round((1 - norm.cdf(3.16))*2,4)))

• p值0.0016低于我们的alpha值0.05，所以我们拒绝了原假设，并告诉我们的客户，是的，似乎新的应用程序设计确实帮助她的用户节省了更多的钱。大功告成!

最后，请注意，我们解析计算的p值为0.0016与我们之前模拟的0.0009是不同的。这是因为我们运行的模拟是单侧的(单侧测试更容易理解和可视化)。我们可以通过将模拟的p值乘以2(考虑到第二个尾巴)来调和这些值，得到0.0018——非常接近0.0016。

结论

在现实世界中，A/B测试不会像我们的例子那样清晰明了。大多数情况下，我们的客户(或老板)不会为我们提供现成的数据，我们将不得不自己收集和清理数据。下面是一些在准备A/B考试时需要记住的实际问题就：

• 您需要多少数据?收集数据既耗时又昂贵。一个运行糟糕的实验甚至可能最终疏远用户。但是如果你没有收集到足够的观察，你的测试就不是很可靠。因此，你需要小心地平衡更多的观察结果和增加的收集成本。
• 错误地拒绝一个真实的零假设(第一类错误)的代价和不拒绝一个虚假的零假设(第二类错误)的代价是什么?回到我们的例子，类型1的错误相当于在新的应用程序设计没有节约效果的情况下给它开绿灯。第二类错误与坚持现行的设计是一样的，而新设计实际上鼓励人们存更多的钱。我们通过选择一个合理的阀值alpha来权衡类型1和类型2的风险。较高的alpha增加了第1种错误的风险，较低的alpha增加了第2种错误的风险。

希望这次演讲能让大家获益良多!

原文作者：Tony Yiu
翻译作者：Chen
美工编辑：过儿
校对审稿：Dongdong
原文链接：https://towardsdatascience.com/data-science-fundamentals-a-b-testing-cb371ceecc27