
长文总结在机器学习中处理倾斜数据集
假如你在公司里被要求创建一个模型,根据你可以使用的各种测量方式,它可以预测产品会否有缺陷。你决定使用你最爱的分类器去在数据上训练模型,结果:你得到了96.2% 准确度 (accuracy)!你老板对结果很惊讶,决定不做任何测试就直接使用你的模型。几周之后他走进你的办公室并强调你的模型多么没用。实际上,自从在生产线上使用了你创造的检测模型后它从来没有发现过任何有缺陷的产品。经过一些调查后,你发现公司制造的产品有大约3.8% 缺陷率,然而你的模型只要总是回答“没有缺陷”就可以达成96.2%准确度。正是因为数据是不平衡的才导致你得到这种简单没用的结果。这篇文章的目的就是回顾可以解决分类模型中倾斜数据问题的不同方法。
我们首先将总结可以帮助检测到“幼稚行为”的不同评测指标。之后我们将讨论一系列重新处理数据的方法以及它们有可能会产生的误导。最后我们会展示在多数情况下重新处理数据是最好的解决办法。
由∞符号表示的一些段落里包含更多的数学方面的细节, 你如果跳过它们并不影响你对整体文章的理解。需要注意的是在接下来的大部分内容中,我们将考虑二元分类问题但是它们可以容易地扩展到多元分类问题。
01 检测“幼稚行为”
在第一节中,为了确保能发现任何种类的“幼稚行为”,我们将展示不同评估分类器的方法。正如我们在引言中的例子所看到的那样,准确度虽然是一个重要且不可避免的指标,但可能会产生误导,因此我们应谨慎利用它,并与其他指标一起使用。让我们看看有没有其他的方法。
混淆矩阵 (confusion matrix),精确度(precision),召回率(recall),F1分数
混淆矩阵对于处理分类问题来说永远是一个简单又不错的指标。这个指标可以很好地概述模型的运行情况。因此它是一个不错的起始点来评估分类问题。我们总结了可以从下图中的混淆矩阵中推导出的大多数指标:
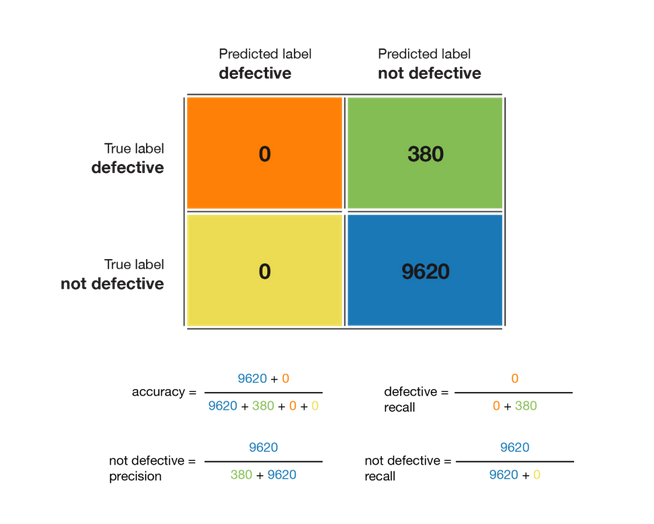
让我们简短地解释下这些指标。模型的准确度基本上是所有正确的预测数/总预测数. 当模型预测一个数据点分类到具体类别时,该类别的精确度可以定义其结果的可信度。而类别的召回率代表了模型对于实际检测该类别的运行情况。一个类别的F1 分数实际上是精确度和召回率的调和平均数,它在同一个指标内融合了精确度和召回率。
对于给定的类别, 精确度和召回率的不同组合可以给出以下不同的意义:
· 高召回+高精确:模型完美地学习了这个类别
· 低召回+高精确:模型不能很好地检测这个类别,但是一旦它预测数据属于这个类别,这个结果非常可信
· 高召回+低精确:这个模型可以很好地检测这个类别,但是同时结果会包含一些数据实际属于其他类别
· 低召回+低精确:模型很难处理这个类别
在我们一开始的例子中,我们构建接下来的混淆矩阵给10000个产品。
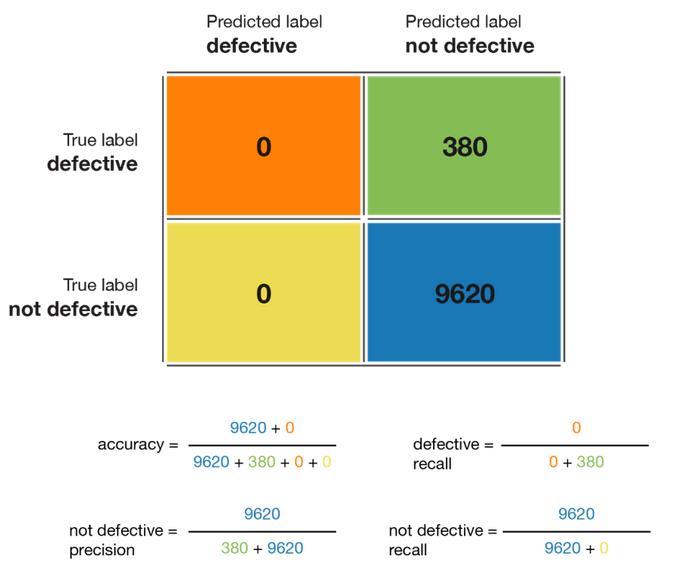
所以准确度是我们之前提到的96.2%。无缺陷组的精确度是96.2% 并且有缺陷组的精确度不能计算。无缺陷组的召回率是1,代表完美预测这个组(所有无缺陷的产品都被标记了没有缺陷)。但有缺陷组的召回率是0,代表更糟糕的情况(任何有缺陷的产品都没有被检测到)。所以我们可以总结出我们的模型没有很好地处理有缺陷组。对于有缺陷产品我们不能计算F1分数, 但是无缺陷组是0.981。在这个例子中,观察混淆矩阵会导致我们重新考虑我们的模型或目标 (正如我们在接下来的章节看到的那样)。它可以帮助阻止我们继续使用没有用的模型。
ROC 和 AUROC/AUC
另一个有趣的指标就是ROC 曲线(代表接收器工作特性:Receiver Operating Characteristic),定义了对应的分类组(我们接下来来用C标注)。
假设对于给定点x,我们有个模型可以给出分类到组C的概率:P(C|x) 。基于这个概率,我们可以定个决策规则,即当且仅当P(C|x) ≥ T 时,x属于C组,其中T是定于决策规则的给定阈值。如果T=1,只有当模型100% 确定时一个点才会被标记成组C里。如果T=0,每一个点都会被标记成在组C里。
阈值T的每一个值都会产生一个点(假阳性,真阳性),然后ROC曲线是当T从1变化到0时产生的点的集合描述曲线。这个曲线从点(0,0)开始增长到(1,1)结束。一个优秀的模型会拥有一个从0快速增长到1的曲线(代表只牺牲很小一部分的精确度来得到高召回率)。
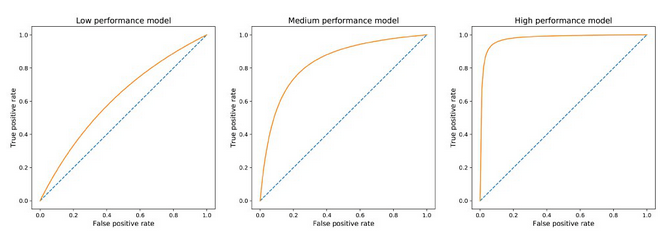
在ROC曲线上,我们可以构建另一个使用简单的指标来评估模型:AUROC或AUC ,ROC下的面积(Area Under the ROC)。AUC 作为标量值(一维)总结了整个ROC。正如所见到,AUC =1代表最好的情况而0.5代表最坏的情况。
同样的情况,一个好的AUC 分数代表我们评估的模型没有牺牲很多精确度来换取更高的召回率在观测组(通常是少数组)。
02 问题究竟是什么?
在尝试处理问题之前,我们可以先试试更好地理解它。我们将考虑一个非常简单的例子,它将使我们快速地检查二元分类的一些基础方面内容并且更好的了解倾斜数据的实质问题。这个例子也将在接下来的章节会被用到。
一个倾斜数据的例子
假设我们有两个分类组:C0和C1. 来自C0组的点遵循均值0和方差4的一维高斯分布 Normal(0,4)。而来自C1组的点遵循均值2和方差1的一维高斯分布 Normal(2,1)。假设在我们的例子中90%的数据来自C0组而剩下10%来组C1。在下图中我们描绘了一个有着上述正确比例和理论分布的包含50个点的代表性数据集。
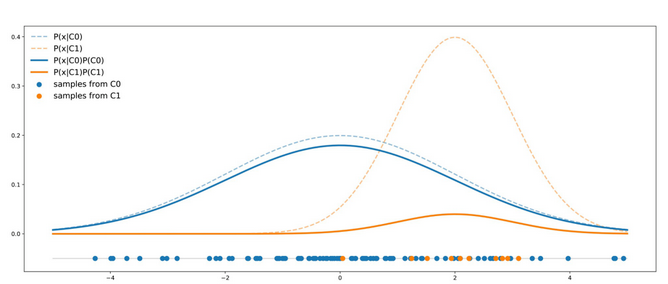
在这个例子中我们可以看到C0组的曲线总是在C1组的上面,所以对于任意点来说,它从C0组中抽出的概率总是高于其从C1组抽出的概率。数学上来说,运用基本贝叶斯定理,我们可以写出
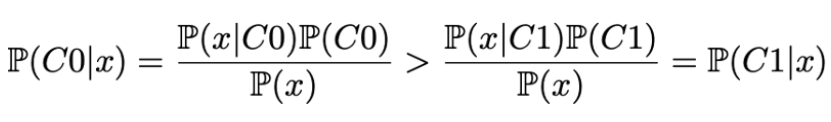
其中我们可以清楚的看到先验概率的影响并且它是如何导致一个类别组的概率总是高于另一个类别组的概率。
所有都意味着即使从完美的理论角度,我们知道如果我们在这些数据上训练分类器,当模型永远回答C0时就会将分类器的准确度最大化。所以,如果目标是取得最好可能的准确度去训练一个分类器,它将不再是个需要解决的问题而是个事实:那就是基于这些特征上,就准确度而言我们能做的最好的就是永远回答C0。我们不得不接受这个事实。
关于分离性
在给定的例子中,我们能观察到两组并没有很好地分离。但是我们能注意到面对不平衡的数据集并不一定意味着两组很好地分离,因此分类器没有在少数类上做的很好。举个例子,假设我们依旧有两个组C0(90%)和C1(10%)。C0的数据遵循均值0方差4的一维高斯分布,而C1的数据遵循均值10方差1的一维高斯分布。如过画之前类似的图,我们就会得到下图
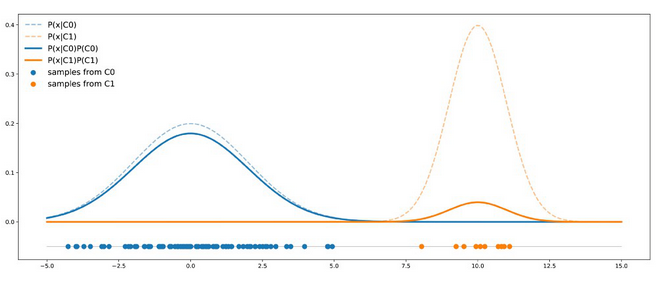
我们可以看出跟之前的例子不同的是C0曲线并不是总高于C1曲线,并且有一部分点会更容易来自C1而不是C0。在这个情况下,两个组非常奋力地很好以至于可以弥补一些不平衡性:一个分类器不会总是回答C0。
理论最小误差概率(∞)
最后我们应该记得分类器有理论最小误差概率。对于这种分类器(一个特征,两个分类组),我们可以通过下图看出理论最小误差概率是两条曲线下的最小面积。
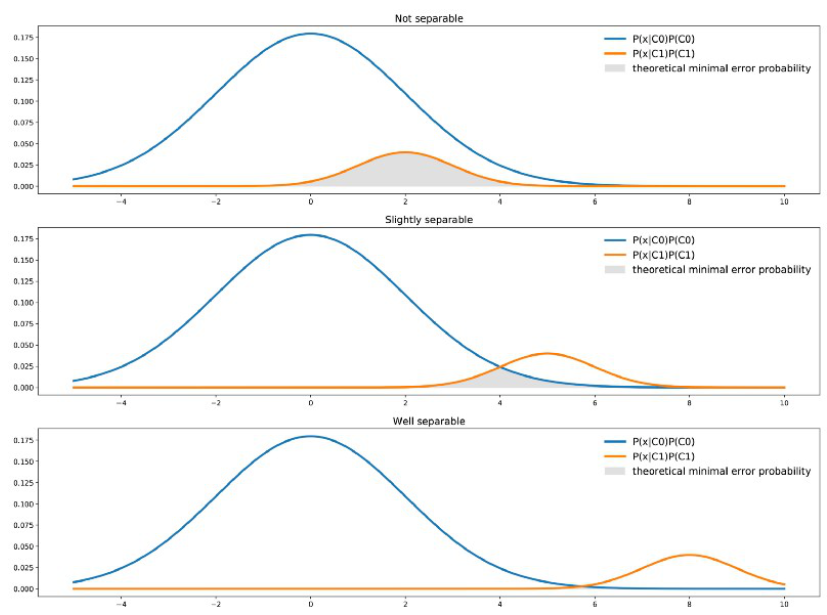
我们可以用数学方法来重现这种直觉。实际上从理论角度来看,最好的分类器会为每个点x在两个类别组中选择最有可能的。它意味着对于给定点x,最好的理论误差概率是由两组中的较小可能性的决定的:
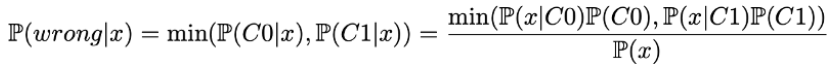
之后我们可以表示所有错误概率:
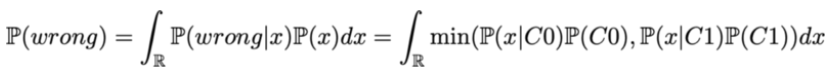
这就是上图中两个曲线下的最小区域。
03 重新处理数据有时无法解决问题
当面对倾斜数据集时,人们最开始可能的反应是考虑数据并没有很好地代表实际现实:如果真的是这个问题,我们其实假设数据实际上是近乎平衡的但这里存在比例偏差(比如数据收集方法上有问题)。在这个情况下,基本上必须尝试收集更有代表性的数据。如果实际生活中数据的确是不平衡的话让我们看看还可以做些什么。在下面两个小节中,我们将展示一些直接涉及到数据本身的处理不平衡性的方法。实际上,我们将讨论欠采样,过采样和合成数据的风险和增加特征的优点。
欠采样,过采样和生成合成数据
在训练分类器之前,这些方法经常被用来作为平衡数据的最好方法。以下是对这些处理数据的方法简述:
· 欠采样是从多数组中进行采样来保留一部分数据
· 过采样是从少数组中采样复制数据来增加基数
· 合成数据生成法从少数组中产生新的合成数据(比如SMOTE方法)来增加基数
所有的这些方法旨在重新或多或少地平衡数据集。但是我们一定必须要让所有组别都有近似相同的数据来重新平衡数据吗?或者是否多数组应该保持最多的代表性。如果一定要这么做,我们应该重新平衡多大比例?
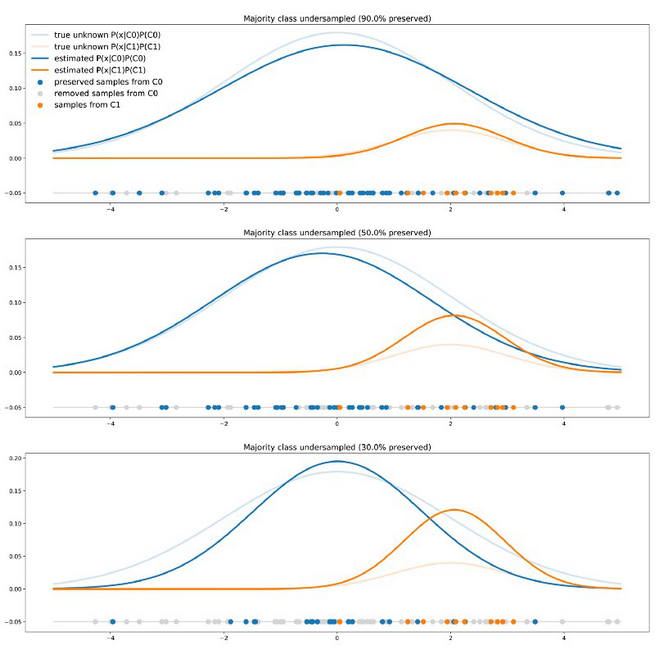
当使用重采样的方法,比如从C0得到多于从C1的数据, 我们在训练过程中给训练器错误的二元组的比例。以这种方式学习的分类器将会在未来实际测试集上得到比在未改变的数据集上训练的分类器更低的准确度。实际上, 分类组的真实比例对于归类一个新数据点来说非常重要,然而当我们重采样整个数据的时候我们会丢失这个信息。
所以,如果这些方法还没有被完全否决掉, 它们应该被小心地使用:如果有目的性地挑选新的比例它就会是个适合的方法,但如果没有深度想过这个问题重新采样没有任何意义。总结这一小节,我们可以说用重采样的方式来调整数据集是在改变现实,所以我们需要谨慎的使用并且清楚分类器之后给出的结果有何意义。
取得额外的特征
我们在之前讨论过取决于分类器的真实目的后重采样训练集(调整分类组比例)有时会是个好办法。如果两个分类组数据不平衡,没有很好地分离并且我们以高准确度作为分类器目标,之后我们得到一个总是回答同一个分类组的分类自并不一定是个问题但是个事实:并没有更好的解决办法。
但是就准确度而言我们依旧可以增加更多特征的方式来丰富数据集来有机会得到更好的结果。让我们回到第一个例子,其中分类组没有很好地分离:也许我们可以找到一个新的特征来帮助区分这两个组并且提升分类器的准确度。
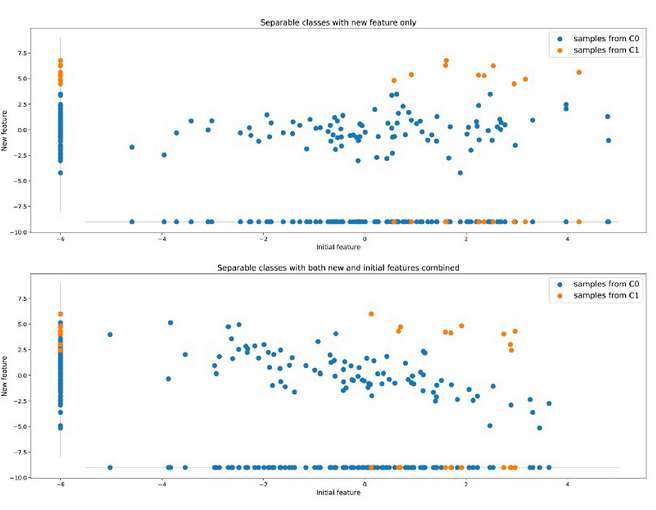
与之前提到的改变数据本质的方法相比,这个方法实际上更好因为它通过从现实中更多的信息来丰富数据。
04 重新处理问题才更有效
到现在为止结论非常令人失望:如果数据代表真实的数据,如果我们不能得到额外的特征并且如果我们需要以准确度为分类器目标,事实是我们总会得到“幼稚行为”(总是回答同一个分类组)。
所以我们依旧对结果不满意吗?在这种情况下以某种方式中我们的问题并没有得到充分的说明(否则我们必须接受这个结果)。我们应该重新处理问题来得到更让人满意的结果。让我们看个例子。
基于成本的分类
没有得到满意的结果来自于目标函数并没有得到充分定义。到现在为止,假设我们以高准确度为分类器评估标准并且期望假阳性和假阴性这两种错误有相同的成本。在我们的例子中这意味着我们假设当真正标签是C1预测成C0与当真正标签是C0预测成C1时一样糟糕。
让我们再次考虑开头关于有缺陷组C1和没有缺陷组C0。我们可以假设对于公司来说没有成功检测到有缺陷的产品(客户服务成本,危险的缺陷导致的可能法律成本等等)比把正常产品错误标记成有缺陷的产品成本(生产成平损伤)更高。
更具体地考虑下我们有了如下的成本:
当真正标签是C1时预测成C0花费P01
当真正标签是C0时预测成C1花费P10 (0<P10 <<P01)
然后我们可以重新定义我们的目标函数:我们想获取更低的预测成本而不再是更高的准确度。
理论最小成本(∞)
理论上来讲,我们想最小化下面给出的预测预期成本其中C(.)定义了分类器方程而不是之前定义的误差概率。

所以如果我们想要最小化预期预测成本,理论上最好的分类器C(.) 最小化了
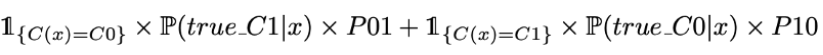
如果除以x的密度就等同于,C(.)最小化了
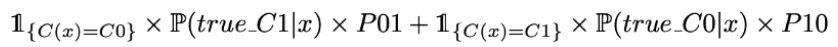
所以有了这个目标函数后,从理论上来讲,最好的分类器将是这样的:
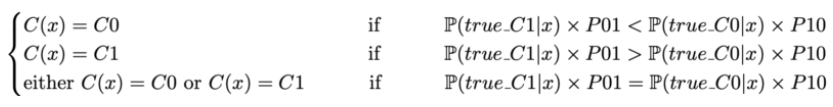
需要注意到的是如果成本是相同的我们会得到基于准确度的经典分类器表达式。
概率阈值
在模型训练之后将成本加入到分类器是第一个考虑成本的方法。首先要用不考虑任何成本的基本的方式训练分类器来得到下面的概率:
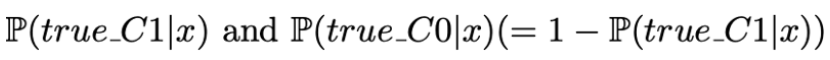
然后预测组将会是C0如果
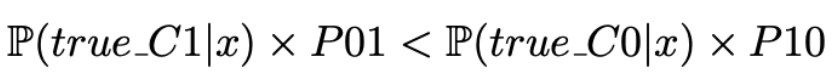
反之C1。
只要它能输出给定点的每个类别的概率,我们使用哪种分类器并不重要。在我们的主要示例中,我们可以用数据来拟合贝叶斯分类器,并且得到的概率将被重新分配比重以便根据描述的成本误差来调整分类器。
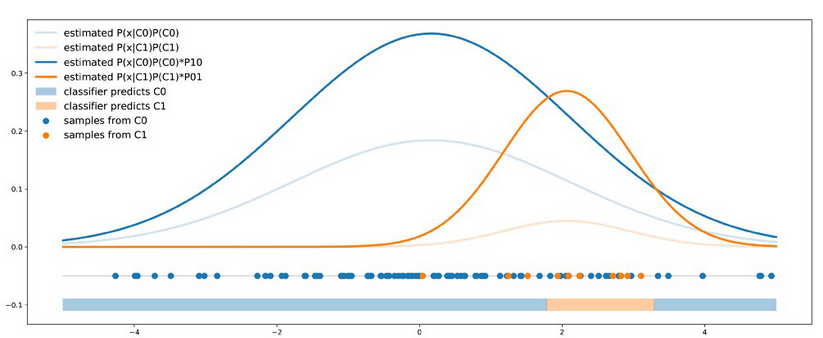
重新加权分类组
重新加权分类组是直接在分类器训练时考虑不均衡成本误差。这样做的话每个类别的产出的概率将会包含成本误差并且能用简单的0.5 阈值来定义分类规则。
对于一些模型来说(比如神经网络分类器),将成本在训练过程中考虑在内会调整目标函数。我们依旧想要我们的分类器得到:
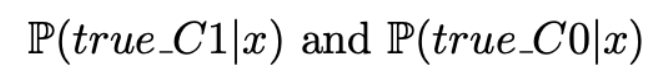
但这次它将会以最小化下面的成本函数来进行训练:
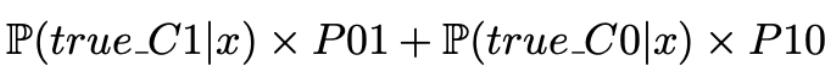
对于其他的一些模型来说(比如贝叶斯分类器),重采样方法可以用来重新加权分类组的比例来让成本误差信息输入到分类组比例中。如果我们考虑到成本P01和P10(比如P01>P10),我们也可以:
以P01/P10的倍数来过采样少数组(少数组的基数乘以P01/P10)
以P10/P01的倍数来欠采样多数组(多数组的基数乘以P10/P01)
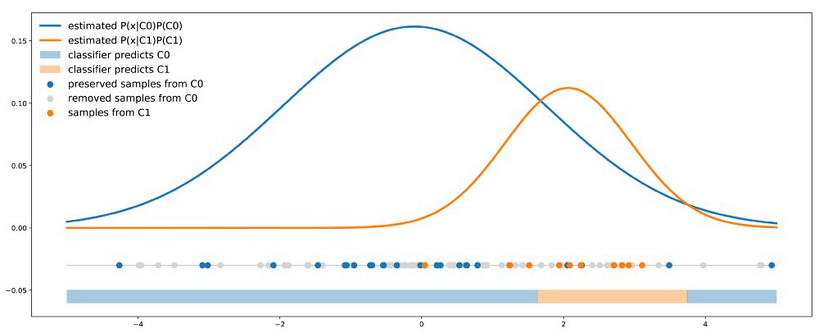
05 精彩回顾
· 无论何时使用一个机器学习算法,模型的评估指标一定要谨慎选择:我们必须使用那些可以最好了解模型在实现目标方面表现的指标。
· 当处理一个不平衡的数据集时,如果分类组没有很好地分离并且如果我们的目标是想得到最好的准确度,最好的分类器就会非常“幼稚”地永远预测成多数组。
· 同样我们可以考虑使用重采样但是必须考虑清楚:他们不应该被用作独立的解决法案而是必须与返工后的问题相结合来实现特定的目标。
· 重新定义问题本身有时候是解决数据倾斜问题的最佳方案:应该设置跟具体目标有关的分类器和决策标准,比如最小化特定成本。
我们应该察觉到我们并没有讨论像分层抽样这样对于批次训练分类器十分有效的方法。当面对数据倾斜时,这样的技巧的确会在训练过程中增加稳定性(通过在同批次的数据中消除来自比例的变化)。
最后总结,这篇文章最大的关键词就是“目标”。了解你确实想要得到的会帮助你克服失衡的数据集并且帮助你得到最可能有用的结果。完美的定义目标总是第一件要事并且也是创建机器学习模型去解决任何事情的起始点。
原文作者:Joseph Rocca
翻译作者:Manxi
美工编辑:Miya
校对审稿:Dongdong
原文链接:https://towardsdatascience.com/handling-imbalanced-datasets-in-machine-learning-7a0e84220f28





