
逻辑回归问题,你解释到点子上了吗?
回归系数本身并不能告诉你需要知道什么。
逻辑回归总是因其可解释性而受到称赞,但在实践中经常被误解。在这些情况下,通常假设逻辑回归模型中的系数与多元线性回归模型中的系数的工作方式相同。但事实并非如此。下面,我们将详细了解逻辑回归的正确解释以及影响特征效果的机制。如果你想了解更多关于数据分析的相关内容,可以阅读以下这些文章:
顺利拿到数据分析师OFFER的作品集长什么样?
Excel小能手们,如何让自己数据分析及汇报的能力再上一层楼?
一篇文章带你了解探索性数据分析
8 种数据挖掘技术,让你成为更好的数据分析师
1958年,David Roxbee Cox在论文中引入了逻辑回归对二元结果建模。今天,它被广泛应用于医学研究、社会科学以及数据科学。当数据科学家开始一个新的分类项目时,逻辑回归通常是尝试的第一个模型。我们用它来感受最重要的特征和方向。然后,如果我们想要提升性能,可能会切换到一个难以解释的分类器,例如梯度提升树或随机森林。如果模型能够进行推理对利益相关者很重要,可以坚持使用逻辑回归。
David Roxbee Cox 爵士发明了用于生存分析的逻辑回归和比例风险模型(以他的名字命名Cox回归)。资料来源:维基共享资源。
在线性回归模型中,系数β通过特征变化一个单位,告诉你因变量改变了多少单位。这种变化不取决于其他特征或其他系数的值,系数本身的水平直接描述了变化的幅度。相比之下,在逻辑模型中,因变量随特征变化而变化是一个函数,它取决于特征本身的值、其他特征的值以及模型中的所有其他系数!
一个具有两个特征的简单模型示例。在线性模型中,预测ŷᵢ只是特征值和系数的加权和。为了简化符号,我们将这个加权和缩写为μi=β0+β1x1i+β2x2i。逻辑回归使用相同的加权和μi,将逻辑函数Λ(x) = exp(x)/[1+exp(x)]包含在周围,因此所有预测都在0和1之间,它可以解释为概率。
线性回归:ŷᵢ = μi
逻辑回归:ŷᵢ = Λ(μi)
通常,系数被解释为当特征值发生微小变化且其他所有特征保持不变时,因变量发生的变化。从数学上讲,这意味着我们正在考虑偏导数。所以这里是两个模型关于第一个系数β1的偏导数:
线性回归:∂ ŷᵢ / ∂ x₁ᵢ = β₁
逻辑回归:∂ ŷᵢ / ∂ x₁ᵢ = Λ(μᵢ)[1-Λ(μᵢ)] β₁
可以看出,β₁本身就是线性回归模型中的偏导数,并没有很复杂。与此相反,与系数值β₁相关的逻辑回归中的边际效应取决于μi,从而取决于x1i、β2和x2i。
由于Λ(μᵢ)和[1-Λ(μᵢ)]都是非负的,β₁的符号决定了边际效应的符号。因此,当我们从多元线性回归中使用时,我们可以解释逻辑模型中特征的影响方向。只有β₁的大小无法直接解释。
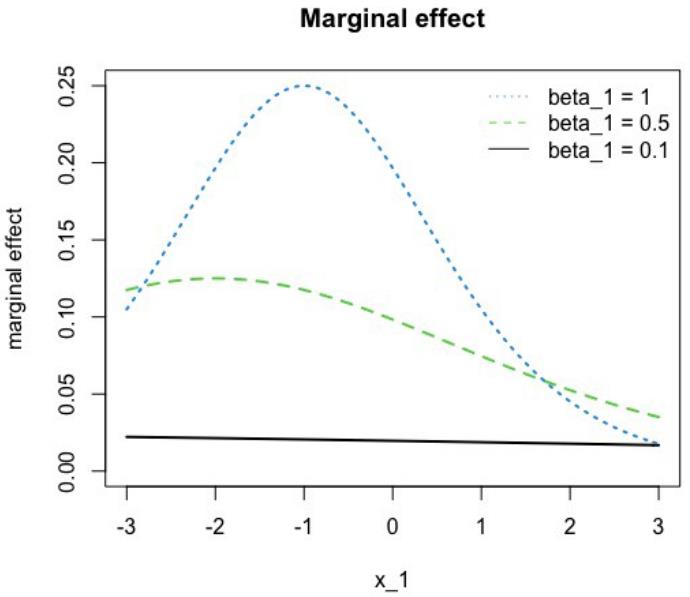
要了解x1i变化对预测结果的影响在多大程度上取决于x1i本身的水平,请查看图 1,下图显示了x1i在固定β0、β2和x2i常数为1的情况下对于不同的β₁值的边际效应。在多元线性回归模型中,边际效应与水平无关,因此所有三条线都只是各自系数水平上的水平线。相反,我们看到影响的幅度要小得多。例如,蓝色曲线的最大值为0.25,即使系数β₁=1。此外,系数越大,非线性越明显。
下面的图2说明了边际效应对其他特征的系数和值的依赖性。这次,固定x1i=1,改变总和β₀+β₂ x₂ᵢ的值。与之前一样,我们可以观察到明显的非线性。
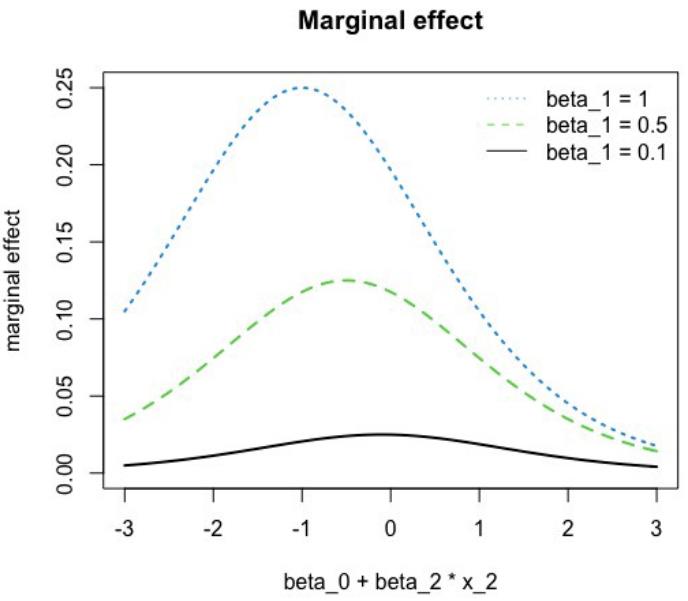
作者提供的图像。
获得更多关于逻辑回归解释的见解,需要注意ŷᵢ是yᵢ的预测,这意味着ŷᵢ给出了yᵢ=1的概率。方程ŷᵢ = Λ(μᵢ)可以反过来看,
μᵢ = Λ⁻¹(ŷᵢ) = ln (ŷᵢ/(1-ŷᵢ))。
这意味着逻辑回归中μᵢ的特征与胜率ŷᵢ/(1-ŷᵢ)的对数之间存在线性关系。
因此,μᵢ中x₁ᵢ和x₂ᵢ对对数几率(log-odds也称为logits)的影响直接由系数β₁和β₂给出。不幸的是,对数几率有点不直观——所以这不能为解释提供良好的基础。
如何做好:平均边际效应和样本均值处的边际效应
基于∂ ŷᵢ / ∂ x₁ᵢ = Λ(μᵢ)[1-Λ(μᵢ)] β₁和μᵢ = β₀ + β₁ x₁ᵢ + β₂ x₂ᵢ有两种方法可以量化x₁ᵢ的边际效应。首先是在x₂ᵢ的平均值处计算导数。这是样本均值的边际效应。这个想法可以随意扩展到任何被认为具有代表性的一组值的边际效应——例如中位数或聚类均值。或者,可以计算样本中每个观察值的偏导数,并报告以这种方式获得的值的平均值。这是平均边际效应。这两种方法都是有效的——它们应该在足够大的样本中给出相似的结果。
确定边际效应的方法有很多——例如R的margins包或Python的statsmodels和sklearn。但是在pyspark.ml中无法实现。
值得一提的特殊情况是,一个或多个特征是虚拟变量(或one-hot编码)。在这种情况下,关于特征的导数∂ ŷᵢ / ∂ x₁ᵢ没有很好地定义。在这种情况下,我们想要使用的是当特征取值为1时与取值为0时预测结果的差异。如前所述,可以在其他特征保持在平均值的同时计算,也可以在取平均值之前对每个观察值进行计算。
在实践中,我们经常使用部分依赖图、累积局部效应、LIME或Shapley值等工具来更好地理解和解释我们的模型。这些与模型无关,也适用于逻辑回归——尽管有人可能会认为,其中一些可以通过边际效应直接解释的东西来说太过分了。然而,这些工具中的每一个都对模型提供了不同的见解,因此它们可以增强我们的理解。如果模型解释的不同方法对某些特征的作用给出了不同指示,通常会特别有启发性。
我个人非常喜欢边际效应,因为它们可以很好地总结每个特征的效果,即使使用更复杂的转换,例如平方项和与其他特征的交互。在这些情况下,只有同时考虑多个特征才能解释原始变量的影响。在这种情况下,边际效应可以很好地延伸。例如,如果我们包含一个平方项,使得μᵢ = β₀ + β₁ x₁ᵢ + β₂ x₁ᵢ²我们有∂ ŷᵢ / ∂ x₁ᵢ = Λ(μᵢ)[1-Λ(μᵢ)] (β₁+2β₂ x₁ᵢ)。
这就是我们在多元线性回归和逻辑回归中系数解释之间关系的完整循环。将逻辑回归模型的系数简单地解释为边际效应是不正确的,这与我们在多元线性回归模型中所做的相同。但在实践中,事情很快变得更加复杂,因为模型很可能包含多项式项和交互项。在这种情况下,多元线性回归和逻辑回归的处理方式相同——我们必须计算边际效应来解释它们。
感谢你的阅读!你还可以订阅我们的YouTube频道,观看大量大数据行业相关公开课:https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ;在LinkedIn上关注我们,扩展你的人际网络!https://www.linkedin.com/company/dataapplab/
参考:
WH Greene (2012):Econometric Analysis, 7th edition, Pearson Education.
T. Hastie、R. Tibshirani和J. Friedman (2009):The Elements of Statistical Learning, 2nd Edition, Springer Science+Business Media.
原文作者:Christian Leschinski
翻译作者:明慧
美工编辑:过儿
校对审稿:Miya
原文链接:https://towardsdatascience.com/are-you-interpreting-your-logistic-regression-correctly-d041f7acf8c7





