三分钟带你走进支持向量机

支持向量机这个算法已经问世很多年了，到现在为止，它的理论和数学推导都已经比较完善，SVM背后伟大的数学理论基础可以说是人类的伟大数学成就，因此SVM的解释性也非神经网络可比。可以说，它的数学理论让它充满了理性，这样的理性是让人向往的。

这就好像，你渴望知道食物的来源以确定食物是否有毒，如果有毒的话，是什么毒，这样的毒会在人体内发生了什么反应以至于让你不适 —— 我的理性驱使我这么想，一个来路不明的食物是不能让我轻易接受的。

支持向量机是一种二分类模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。简而言之，SVM就是要在两类数据点中寻找一个超平面，使得两类数据点中距离最近的点之间的距离最远。

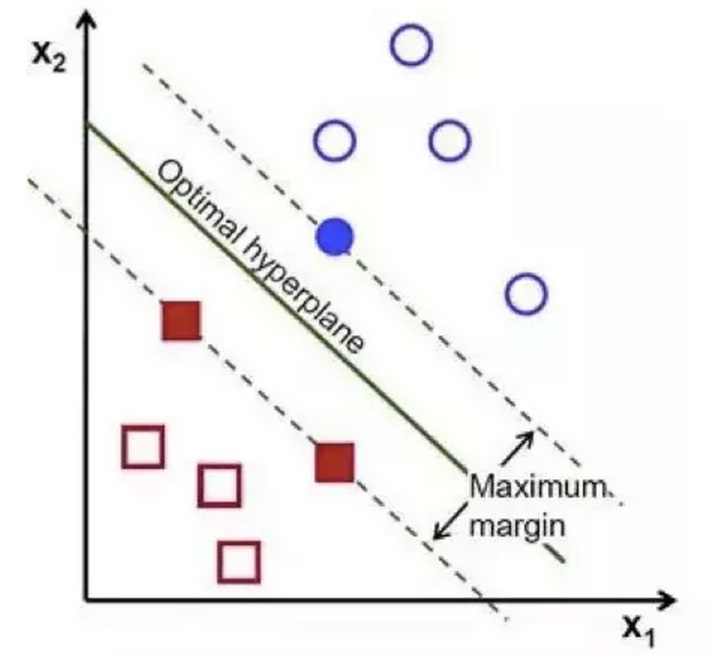
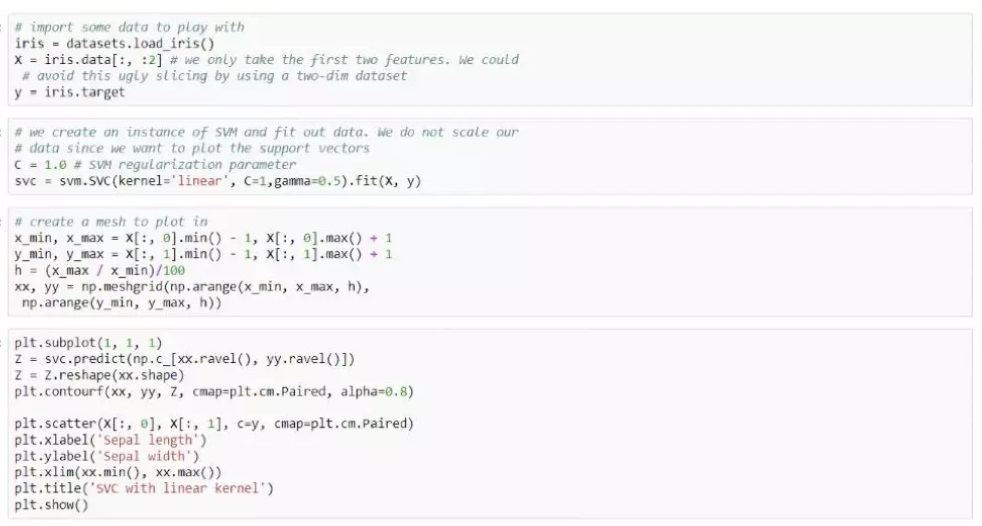
俗话说以练代学，我们先来看看它如何使用。

如上图👆所示，短短几行代码，就可以调用Python sklearn中的SVM模型，使用它预测数据了。那么，我们为什么还要花时间了解它背后的数学原理呢？

首先，如果想进行SVM的理论研究，完善已经开源的代码的话，了解其背后的数学原理是必不可少的。

其次，即使单纯在工业界应用SVM来解决分类或者回归问题，也需要了解模型的推导过程，以及这个模型中每个参数的意义，才能在初步建模之后的调参过程中，达到自己想要的效果。

然后我们基于Python中自带的iris dataset进行一个简单的case study，让大家看一下SVM的实现效果以及调参过程。

SVM的模型中，有三个参数比较重要，分别是kernel, c和gamma，其中gamma是rbf kernel 特有的参数。

Kernel,也就是核函数，决定了SVM的分类方式。常用的kernel有linear kernel, polynomial kernel和rbf kernel。下图就是我们使用linear kernel的分析结果，得到了线性的分界线。下图就是我们使用rbf kernel得到的结果，是一个曲线的分界, polynomial同样也是如此。

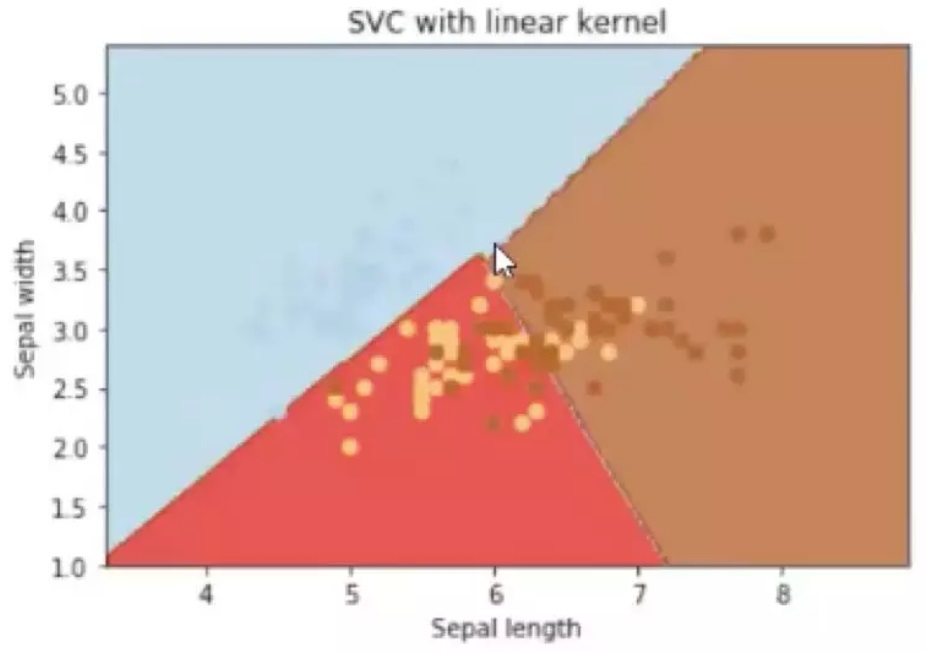
之前提过，gamma是rbf kernel很重要的一个参数，我们就来看一下不同的gamma条件下得到的结果有什么区别。

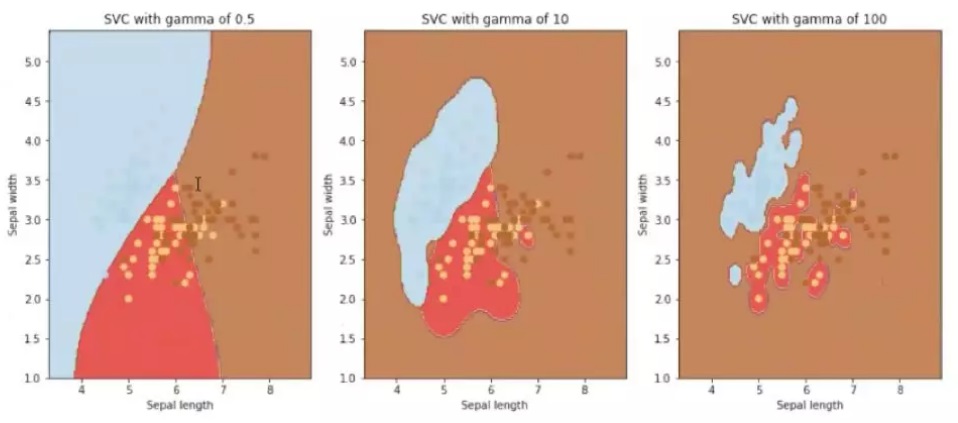
很明显，gamma越小，得到的超平面越平滑，分类越不彻底，越容易underfitting; gamma越大，得到的超平面越凹凸不平，像缩水一样逐渐收缩，分类对training set的依赖性越强，越容易overfitting。

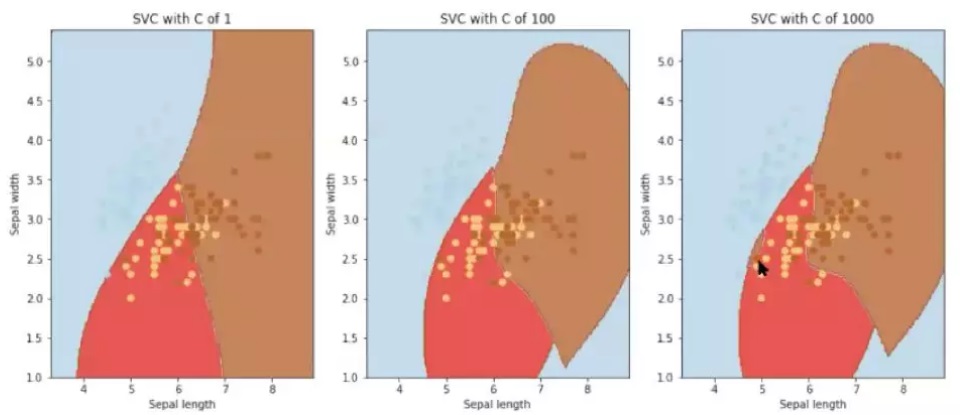
参数C，也就是松弛向量，是每个SVM的模型都有的一个参数，其效果和gamma有异曲同工之妙。随C值的由小到大，函数会变得越来越复杂，越来越收敛，会局限到某一个区间内。换句话说，当C值越大的时候，模型会更看重对噪音点的判别（如图鼠标所指的地方），更容易overfitting。而当C值越小，对噪音的容忍度就越高，有可能underfitting。

说了这么多，SVM到底是如何实现的呢？

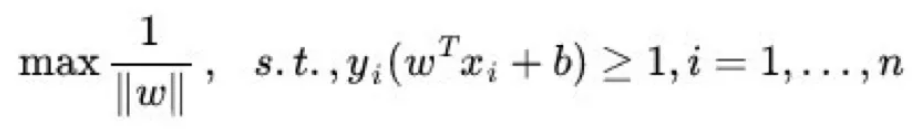
这就是SVM问题的基本型。

可能有同学会问，如果原始样本不存在一个能正确划分出两类样本的超平面，怎么办呢？

于是引入了一个新的概念：核函数。它可以将样本从原始空间映射到一个更高维的特质空间中，使得样本在这个新的高维空间中可以被线性划分为两类，即在空间内线性划分。这个过程可以观看视频感受感受：https://www.youtube.com/watch?v=3liCbRZPrZA