
Correlation相关性 VS Regression回归:它们有什么区别?
在进行机器学习时,在你在键盘上移动手指并开始编程之前,有很多名词需要你提前理解。这些名词不仅与“可用的”算法有关,而且与数学概念非常相关。
在研究数据科学和机器学习时,你需要了解统计学中的一些名词;其中,有两个名词是相关性(Correlation)和回归(Regression)。在这篇文章中,我将用具体例子解释这两个名词之间的区别。如果你想了解更多关于机器学习的相关内容,可以阅读以下这些文章:
5种有效方法:提高机器学习模型的准确性
机器学习的一站式library清单
你知道吗?SQL也能做机器学习!
群体学习(Swarm Learning)的工作原理——结合区块链和机器学习的更优解决方案
1.相关性(Correlation)
一句话来说,相关性就是表示两个变量之间线性关系的统计度量。
就是这样简单。但是,我们需要把定义付诸于实践(同时也能更好地理解我们正在研究的这个名词)。
深入这个概念,我们可以说,如果第一个变量的每一个值,都遵循一定的规律性对应于第二个变量的一个值,那么两个变量是相关的;因此,如果两个变量高度相关,路径将是线性的(一条线),因为相关性描述了变量之间的线性关系。
也就是说,相关性表示的是变量之间的关系,而不是因果关系!如果自变量的值增加,而因变量的值也增加,但这并不意味着第一个变量导致了第二个变量值的增加!
让我们举个例子:
现在是夏天,天气很热;你不喜欢你所在城市的高温,所以你决定去山上。幸运的是,你到达山顶,测量温度,你发现它比你所在城市的温度低。你会有点疑惑(因为你对气温的下降不理解),于是决定去一座更高的山,发现那里的气温甚至比前一座山上的还要低。
你尝试不同高度的山脉,测量温度并绘制图表;你会发现,随着山的高度增加,温度降低,你可以看到一个线性趋势。这是什么意思?这意味着温度与高度有关;这并不意味着山的高度导致了温度的下降(如果你用热气球到达同一高度、同一纬度,你会测量出什么温度?)。
所以,既然在物理世界中,我们需要定义来衡量事物,一个好问题是:我们如何衡量相关性?
测量相关性的典型方法是使用相关系数(也称为皮尔逊指数Pearson index或线性相关指数linear correlation index)。这里我们不讨论数学,因为这篇文章的目的是提供和普及信息,而不是公式:我想让你抓住并理解概念。
相关系数利用了协方差的统计概念,这是一种定义两个变量如何一起变化的数值方法。撇开数学只谈概念,相关系数是一个介于-1和+1之间的数值。如果相关系数为-1,这两个变量将具有完美的负线性相关;如果相关系数为+1,两个变量将具有完美的正线性相关;如果相关系数为0,则表示这两个变量之间没有线性相关性。
因为我们需要做数据科学工作,让我们一起看一下代码。我们如何在Python中计算相关系数呢?我们通常会计算相关矩阵。假设我们在一个名为“df”、“Variable_1”和“Variable_2”的数据框中存储了两个变量,我们可以绘制相关矩阵,例如在seaborn中:
import seaborn as sns
#heat map for correlation coefficient
sns.heatmap(df.corr(), annot=True, fmt="0.2")我们会得到:

上图显示,我们考虑的两个变量高度相关,因为它们的相关系数为0.96。然后,我们希望用一条具有正斜率的直线来描述它们之间的关系。现在我们来讨论下一个概念:回归regression。
在讨论回归的概念之前,我想说最后一件事。在本文中,我强调了一个事实,即相关性与变量之间的线性关系有关。让我们假设两个变量,我们确信它们不是线性相关的;例如:
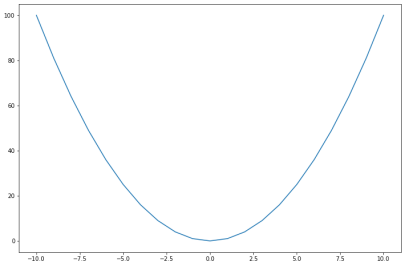
在这种情况下,如果我们计算相关系数,我们得到0:

上面变量不相关的事实告诉我们,没有单纯的一条线可以描述变量之间的关系:但这并不意味着变量根本不相关!这只是意味着这种关系不是线性的。
2.回归(Regression)
回归分析是一种数学技术,用于分析一些数据,包括一个因变量和一个(或多个)自变量,目的是找到因变量和自变量之间的最终函数关系。
回归分析的目的是找到在因变量和自变量之间的一个估计值(一个好的估计值!)。从数学上讲,回归的目的是找到最适合数据的曲线。
当然,最适合数据的曲线可以是直线;但它也可以是任何曲线,这取决于它们之间是何种关系!
所以,我们要做的是计算相关系数,如果它的值接近1,我们可以在研究回归时得到一条直线;否则,我们必须尝试多项式回归(或其他方法,比如指数回归或其他任何方法)!
如果我们计算之前看到的数据之间的回归线(相关系数为0.96的“Variable_1和Variable_2”),我们得到:
import seaborn as sns
import matplotlib.pyplot as plt
#plotting the time series analysis with a red regression line
sns.regplot(data=df, x="Variable_1", y="Variable_2", line_kws={"color": "red"})
plt.xlabel('Variable 1', size=14)
plt.ylabel('Variable 2', size=14)
plt.title('(LINEAR) REGRESSION BETWEEN TWO VARIABLES')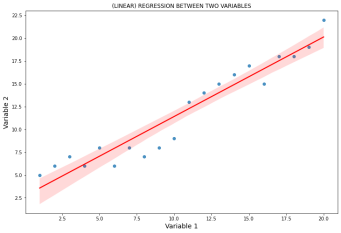
像我们预期的那样,由于变量的相关指数为0.96,我们得到了一条正斜率的直线,作为最适合数据的曲线。
最后,我想说的是,有很多方法可以找到最适合数据的曲线;最常用的方法之一是“普通最小二乘法(Ordinary Least Squares)”。
谢谢你的阅读。希望通过本文,你已经初步理解了这些概念,欢迎在文章评论区讨论补充!你还可以订阅我们的YouTube频道,观看大量大数据行业相关公开课:https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ;在LinkedIn上关注我们,扩展你的人际网络!https://www.linkedin.com/company/dataapplab/
原文作者:Federico Trotta
翻译作者:Chuang Zhang
美工编辑:过儿
校对审稿:Jiawei Tong
原文链接:https://levelup.gitconnected.com/the-2-types-of-software-engineers-every-successful-product-team-needs-11952e937def





