
所有数据科学家都应该知道的三个常见假设检验
假设检验是推论统计学中最基本的元素之一。在像Python和R这样的现代语言中,进行这些检验往往很容易——通常只需要一行代码。但令我困惑的是,很少有人使用它们或理解它们的工作原理。
在本文中,我想用一个例子来展示三个常见的假设检验及其工作原理,以及如何在R和Python中运行它们,并理解结果。如果你想了解更多关于Python的相关内容,可以阅读以下这些文章:
Excel中的Python:将重塑数据分析师的工作方式
5个超棒的Python项目!
数据科学家提高Python代码质量指南
从优秀到卓越:数据科学家的Python技能进化之路
假设检验的一般原则和过程
假设检验之所以存在,是因为当我们试图对一个整体做出结论或推断时,几乎不可能观察到整个总体。几乎总是,我们都是在从整体中抽取样本数据的基础上做出推断。
考虑到我们只有一个样本,我们永远无法对我们想要做出的推断百分之百确定。我们可以确定90%、95%、99%、99.999%,但永远不会是100%。
假设检验本质上是计算我们对基于样本的推断的确定程度。最常见的计算过程有几个步骤:
- 假设推断在总体上不成立——这被称为零假设
- 计算样本上的推断量
- 了解该统计量周围抽样误差的预期分布
- 使用该分布来理解样本统计量与零假设一致的最大可能性
- 使用选定的“可能性截断值”(即alpha)来做出接受或拒绝零假设的二元决策。最常用的alpha值为0.05。也就是说,如果零假设使我们的样本统计量的最大可能性小于1/20。我们通常会拒绝零假设。
销售人员数据集
为了说明本文中的一些常见假设检验,我将使用销售人员数据集,可以在此处获取(http://peopleanalytics-regression-book.org/data/salespeople.csv)。让我们在R中下载它,快速看一下前几行。
url <-"http:://peopleanalytics-regression-book.org/data/salespeople.csv"
salespeople <- read.csv(url)head(salespeople)
## promoted sales customer_rate performance
## 1 0 594 3.94 2
## 2 0 446 4.06 3
## 3 1 674 3.83 4
## 4 0 525 3.62 2
## 5 1 657 4.40 3
## 6 1 918 4.54 2我们看到四列数据:
- promoted — 表示销售人员在最近的晋升轮中是否被晋升的二进制值
- sales — 销售人员最近的销售额(以千美元为单位)
- customer_rate — 客户对销售人员的最近平均评分,评分范围为1到5
- performance — 销售人员的最新绩效评级,其中1是最低级别,4是最高级别。
例1 -Welch’s t检验
Welch’s t检验是一种假设检验,用于确定两个总体是否有不同的均值。这个检验有多种变体,但我们将看一下双样本版本,并询问在总体中,高绩效销售人员是否比低绩效销售人员产生更高的销售额。
我们首先假设零假设,即在总体中高绩效和低绩效销售人员之间的平均销售额差异为零或更小。现在计算样本的均值差异统计量。
library(dplyr)
# data for high performers
high_sales <- salespeople |>
filter(performance == 4) |>
pull(sales)
# data for low performers
low_sales <- salespeople |>
filter(performance == 1) |>
pull(sales)
# difference
(mean_diff <- mean(high_sales) - mean(low_sales))
## [1] 154.9742所以我们看到,在我们的样本中高绩效销售人员的销售额比低绩效销售人员多约15.5万美元。
现在,我们假设销售额是一个随机变量——也就是说,一个销售人员的销售额与另一个销售人员的销售额是独立的。因此,我们预计两组之间的平均销售额的差异也是一个随机变量。所以我们期望真实的总体差异在以样本统计量为中心的t分布上,这是基于样本的正态分布的估计。为了得到精确的t分布,我们需要自由度——这可以根据Welch-Satterthwaite方程(在本例中为100.98)来确定。我们还需要知道均值差的标准差,我们称之为标准误差,我们可以计算为33.48。有关这些计算的更多细节,请参阅此处(https://peopleanalytics-regression-book.org/found-stats.html)。
知道了这些参数,我们就可以围绕我们的样本统计数据创建一个t分布图。。
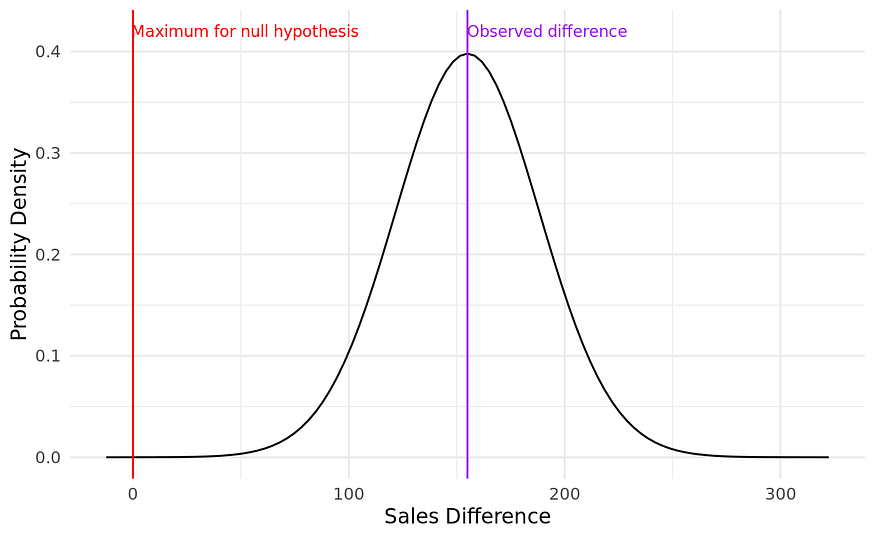
现在我们可以看到真实总体统计量的期望概率分布。我们还可以标记此分布上代表零或更小差异的最大位置-这是我们的零假设陈述。通过计算红线左侧分布下的面积,我们计算出零假设成立时该样本统计量出现的最大概率。通常,这是通过计算达到红线所需的标准误差的数量来计算的-称为t统计量。在这种情况下是:
# standard error
se <- 33.48(t_statistic <- (0 - mean_diff)/se)round(t_statistic, 2)
## [1] -4.63
红线距离样本统计量有4.63个标准差。我们可以使用R中的一些内置函数来计算该t统计量在100.98自由度的t分布下的曲线下的相关面积。这表示我们的样本统计量在零假设下出现的最大概率,并且被称为假设检验的p值。p_value <- pt(-4.63, 100.98)round(p_value, 6)
## [1] 5e-06因此,我们确定样本统计量在零假设下发生的最大概率是0.000005,甚至比非常严格的alpha还要小得多。在大多数情况下,这将被认为太不可能接受零假设,我们将拒绝它,支持备择假设-即高绩效销售人员比低绩效销售人员产生更高的销售额。
要在R中运行这个双样本的t检验,可以使用带有”greater”的t.test函数作为备择假设。在下面的输出中,你将看到我们上面讨论的各种统计信息。
t.test(high_sales,low_sales, alternative = "greater")
## Welch Two Sample t-test
##
## data: high_sales and low_sales
## t = 4.6295, df = 100.98, p-value = 5.466e-06
## alternative hypothesis: true difference in means is greater than ## 0
## 95 percent confidence interval:
## 99.40204 Inf
## sample estimates:
## mean of x mean of y
## 619.8909 464.9167要在Python中运行这个双样本t检验,可以使用scipy.stats版本1.6.0或更高版本。
import pandas as pd
from scipy import stats
# get data
url = "http://peopleanalytics-regression-book.org/data/salespeople.csv"
salespeople = pd.read_csv(url)
# get sales for top and bottom performers
perf1 = salespeople[salespeople.performance == 1].sales
perf4 = salespeople[salespeople.performance == 4].sales
# welch's independent t-test with unequal variance
ttest = stats.ttest_ind(perf4, perf1, equal_var=False, alternative = "greater")
print(ttest)
## Ttest_indResult(statistic=4.629477606844271, pvalue=5.466221730788519e-06)例2 -相关性检验
另一个常见的假设检验是检验两个数值变量之间是否存在非零相关性。
让我们来看看在销售人员数据集中,sales和customer_rate之间是否存在非零相关性。像往常一样,我们假设零假设,即这些变量之间没有相关性。然后我们计算样本相关性:
(sample_cor <- cor(salespeople$sales, salespeople$customer_rate, use = "pairwise.complete.obs"))
## [1] 0.337805同样,我们期望真实的总体相关性在这个样本统计量周围形成一个分布。像这样的简单相关性预计会观察到一个n-2自由度的t分布(在本例中为348),标准误差约为0.05。和之前一样,我们可以画出这个图,并定位我们的零假设红线:
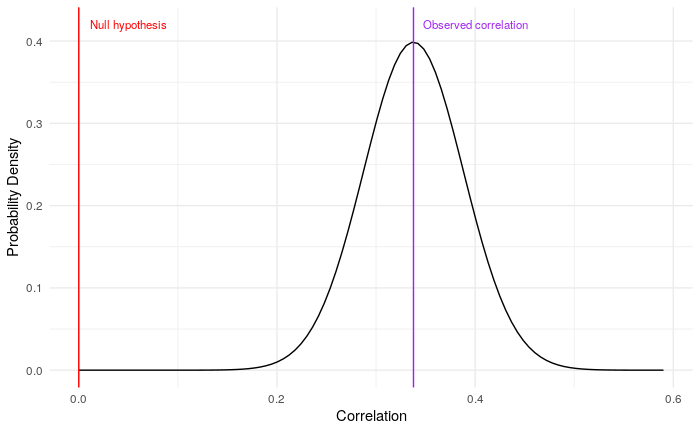
我们看到,红线距离观察到的统计量超过6个标准误差,我们可以计算p值,我们再次期望它非常小。因此,我们可以再次拒绝零假设。
在R中运行:
cor.test(salespeople$sales, salespeople$customer_rate, use = "pairwise.complete.obs")
## Pearson's product-moment correlation
## data: salespeople$sales and salespeople$customer_rate
## t = 6.6952, df = 348, p-value = 8.648e-11
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.2415282 0.4274964
## sample estimates:
## cor
## 0.337805在Python中运行:
import numpy as np
# calculate correlation and p-value
sales = salespeople.sales[~np.isnan(salespeople.sales)]
cust_rate = salespeople.customer_rate[~np.isnan(salespeople.customer_rate)]
cor = stats.pearsonr(sales, cust_rate)
print(cor)
## (0.33780504485867796, 8.647952212091035e-11)例3 -比例差异的卡方检验
与前两个例子不同,数据科学家经常需要处理分类变量。一个常见的问题是,不同类别的变量之间是否存在比例差异。卡方检验是为此目的设计的假设检验。
我们来问一个问题:不同绩效类别的销售人员得到晋升的比例是否有差异?
同样,我们假设零假设,即所有绩效类别中获得晋升的销售人员比例是相同的。
让我们通过创建绩效和晋升的列联表或交叉表来查看每个绩效类别中晋升的销售人员的比例。
(contingency <- table(salespeople$promoted, salespeople$performance))
## 1 2 3 4
## 0 50 85 77 25
## 1 10 25 48 30现在我们假设类别之间是完全平等的。我们通过计算晋升销售人员的总体比例,然后将该比例应用于每个类别的销售人员数量来实现这一点。这将得到以下预期的理论列联表:
## 1 2 3 4
## 0 40.62857 74.48571 84.64286 37.24286
## 1 19.37143 35.51429 40.35714 17.75714然后,我们对观察到的和预期的列联表的每个条目使用这个公式,并将结果相加成一个称为卡方统计量的统计量。
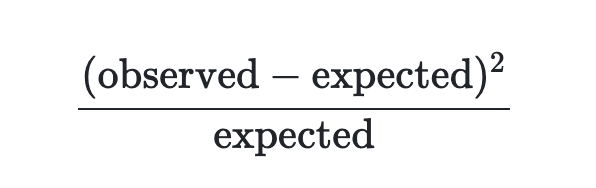
在这种情况下,卡方统计量计算为25.895。
与前面的t统计量一样,卡方统计量的期望分布取决于自由度。自由度的计算方法是从列联表的行数和列数分别减1并相乘——在这种情况下,自由度为3。
和之前一样,我们可以画出自由度为3的卡方分布图,标记出卡方统计量在该分布中的位置然后计算该点右侧分布曲线下的面积,以找到相关的p值。
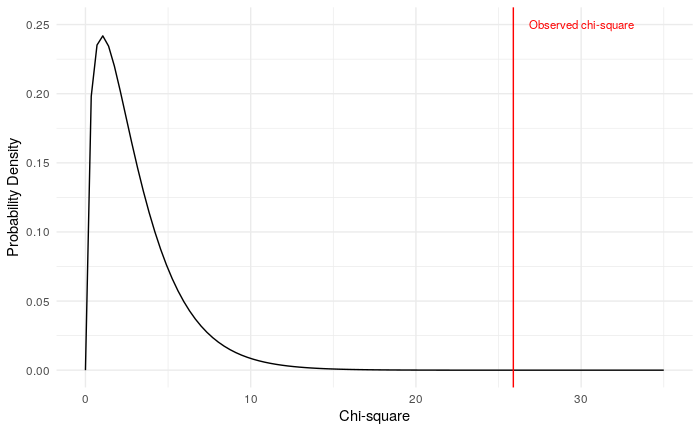
同样,我们可以看到这个区域面积非常小,这表明我们可能会拒绝零假设,并确认备择假设,即不同晋升类别之间的晋升率存在差异。
在计算完列联表后在R中运行:
chisq.test(contingency)
## Pearson's Chi-squared test
##
## data: contingency
## X-squared = 25.895, df = 3, p-value = 1.003e-05在Python中运行它-结果中的前三个条目分别表示卡方统计量,p值和自由度:
# create contingency table for promoted versus performance
contingency = pd.crosstab(salespeople.promoted, salespeople.performance)
# perform chi-square test
chi2_test = stats.chi2_contingency(contingency)
print(chi2_test)
## (25.895405268094862, 1.0030629464566802e-05, 3, array([[40.62857143, 74.48571429, 84.64285714, 37.24285714],
## [19.37142857, 35.51428571, 40.35714286, 17.75714286]]))我希望这些解释和演示对你有所帮助。感谢阅读!你还可以订阅我们的YouTube频道,观看大量大数据行业相关公开课:https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ;在LinkedIn上关注我们,扩展你的人际网络!https://www.linkedin.com/company/dataapplab/
原文作者:Keith McNulty
翻译作者:文玲
美工编辑:过儿
校对审稿:Jason
原文链接:https://keith-mcnulty.medium.com/three-common-hypothesis-tests-all-data-scientists-should-know-d1f1049ef991




