
关于C罗“冲刺速度”这种隐私问题,我们在Kaggle上找到了数据集,然后。。。
你知道 FIFA 么?在线踢足球那种,贼老多人玩儿这个游戏,本仙女作为非深度玩家却总是有技能狂胜各路资深玩家。我并不是个小心机策略怪,我更喜欢看我操控的球员匹配使用冲刺速度,难以捉摸的突然跑位和转向。这些方法让我能够在对方半场制造空缺,顺利运球到位。
为了让我的战术更稳定地发挥,也让我的战术拥有数据支持,我决定发挥一下我的技能,于是我寻找了 Kaggle 上的数据集:FIFA 19 complete player dataset (后台回复 FIFA 获取数据集下载链接)
今天这篇文章,就让我给你细细描述如何用这些可爱的数据们根据变量和特点预测出球员的速度,毕竟这可能是世界上存在的最好战斗攻略了。
第一趴:线性回归
线性回归可以概括为试图模拟一个或多个自变量与特定结果或因变量之间的关系。为使该算法有效,独立变量和因变量之间必须存在线性关系。应用于数据的是两个或多个变量之间存在的中等到强的相关性,它可以通过找到一条最拟合结果的线来进行结果预测,这是个非常有用的起点。
Y = MX +B
这背后的数学很简单,特别是在你只看一个自变量的情况下。Y表示结果或因变量,而M表示斜率,X表示自变量,B表示y轴截距。简单地说,假设X和Y之间存在线性关系,如果你知道线的斜率和自变量的价值,你可以预测结果。然而在我的情况下,我将查看多个独立变量,因此所需的公式稍有变化。
F(x) = A +(B1*X1) +(B2*X2)+(B3*X2)+(B4*X4)…+(Bn*Xn)
有了这个公式,我假设我需要考虑n个自变量。在这种情况下,F(x) 是该线性模型的预测结果,A是y轴截距,X1到Xn是预测变量/自变量,B1到Bn是回归系数 (相当于简单线性回归中的斜率)。在这个公式中代入相应的数字后得出预测结果,在这个例子中,是玩家在FIFA19上的冲刺速度。
第二趴:与数据进行“心连心的交流”
我选择使用Python去分析,从 Kaggle 上下载数据,将其上传到我的 Google 云端硬盘,加载到 Google Colab 并使用 pandas 的 read.csv 函数上传数据。在加载了scipy,numpy和 pandas 库后,我将继续进行数据清理。

第三趴:数据清理
我开始时先做了些假设,我认为冲刺速度很大程度上受高度,重量,年龄,加速度以及球员的体重和身高之间的比例的影响。在观察数据集时,我注意到高度和重量以字符串格式记录(比如5’11和180lbs),另外作为更习惯公制度量标准的人,我想将这些测量值分别改成厘米和千克。

对于体重来说,这个单位转换过程包括通过查找撇号作为分隔符来拆分字符串,将其转换为句点(小数点分隔符)并应用lambda函数将字符串格式(string)转换为浮点型格式(float)并将其转换成厘米。我将字符串转换为浮点数是因为我知道计算会返回一个基本上是浮点型的数字。
执行此操作后,我将继续使用数据中的平均高度值填充所有NaN值,并将数字转换为整数(小于100行)。我的假设是用平均值填充缺失值对于我的分析比向前填充,省略NaN行数据或将其更改为0更好。我后来才知道这些列不适用于我的分析,但是我决定将其包含在内来展示我必须做的数据列清理工作。

在将相同的清理应用到高度的数据列后,我定义了一个函数应用于列,使用该列的平均值填充所有的NaN值并将该数字转换为整数格式(int)。在我用于分析的数据列上测试后,我在相关数据列上应用了这个函数。
第四趴:检测相关性和显著性测试
为了测试每列和结果列(冲刺速度)之间的相关性,我选择使用scipy包中的spearmanr函数。该函数计算相关性并返回x和y之间的相关性以及p值或该相关性的显著性概率。

使用此函数,我遍历了数据集中的不同列,以确定我将用于回归模型的列。我选择使用存在至少0.50或低于-0.50的中等到强相关的列。用这个基准我得到了我需要的自变量的列:敏捷,加速,平衡,定位,技能移动,控球,交叉,整理和反应。
通常当你测量线性时,你可能需要使用散点图来可视化每一列来确定线性关系确实存在。纯粹依赖于相关系数有个问题,有影响的异常值可以显著地增大或减小相关系数,使得当实际不存在什么相关性时看起来好像有强/弱相关。通过了解球员得分如何在国际足联中分布,我假设并不需要考虑这个问题,我们不会得到极具影响力的奇异值(除了销售价格之类的列)。
第五趴:多元线性回归模型

我的机器学习算法(假设你考虑使用一个线性回归机器学习模型)主要依赖于sklearn库。在导入这个库后,我选择应用80/20规则来划分数据成训练集和测试集,我认为我不想使用超过20%的数据以便更加确定我的模型可以推广到整个数据集。

我继续定义我想在模型里使用的特征或自变量和我想预测的目标或因变量,并且训练用线性回归训练我的模型。训练涉及到查看自变量与因变量之间的相关性,以及进行计算来使模型能够预测测试数据的结果。
第六趴:测试模型
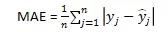
为了测试数据集的预测误差(损失函数)我使用了sklearn里的指数模块来计算训练集和测试集的平均绝对误差MAE。在这个公式里n代表了数据里的误差数,Σ代表了加和,代表了每个观察值和预测值的绝对误差。这个公式把所有绝对误差相加并除以总观察数,返回一个代表预测值和实际冲刺速度的平均绝对误差的数字。
理想情况下,我希望得到的MAE尽可能的小,并且与我的预测成功率结果一起报告。我可以选择使用类似于MAE的均方根误差RMSE,同样返回一个显示预测值与预测值的偏差的数字。RMSE 只是找到MAE的平方根(但是我们会在这个例子中对绝对误差进行平方)。

为了测试这个模型的准确性,我选择运用了r2_score_metric(coefficient of determination 确定系数)。R2 Score 或 R-squared 衡量数据与回归模型的拟合程度,数字越接近1模型越接近,表明线性回归模型解释了相当大比例的数值-表明预测能力更强。
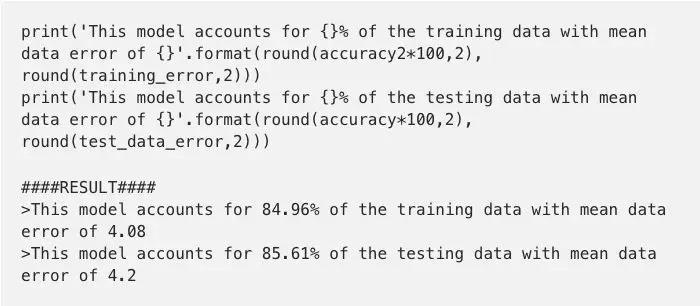
正如我的控制器报告,预测模型解释了我测试数据的85.61%,平均偏差大约4.2(预测值与实际值之间的平均偏差)。举个例子,根据结果,如果我们使用该模型对冲刺速度为90的玩家进行预测,则实际冲刺速度平均在86和94之间的概率非常大。
根据R-squared的理解,我为我的模型加入越多的预测变量,R-squared值会增加,因为我会在数据里考虑更多的变化。考虑到这一点,我可以看调整后的R-squared值,它会惩罚更多预测因此的使用,这种惩罚的大小取决于预测因子的数量与数据中有可能的预测因子(所有其他列)的大小之间的关系。
结果是只有当添加的预测变量使模型比偶然的预期提升更大时,调整过的R-squared值(adjusted R-squared)才会增加。
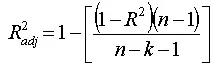
在上述公式中,k代表了预测变量的数量而n代表数据中的总列数。

在我想测试此模型与其他模型的适合度的情况下,此百分比将变得更有用。
我注意到使用预测因子的另一个问题是,一些预测因子与其他预测因子产生多重共线性。但是根据我的理解,这对我的模型的预测能力没有显著影响,它对估计每个预测器对我的模型的影响的能力有更大的效果
第七趴:做出预测
现在让我们设想使用这个模型来进行实际预测。我们在数据里随机选择一个选手。这恰好是现年21岁,英格兰出生的约瑟夫•亚尔尼。这个选手正好出现在我的测试集里的第26行。

我继续定位这个选手并且提取相关统计信息以josef_stats这个变量进行记录。然后我用创造的多元线性回归公式来对选手的冲刺速度进行预测,得到了预测冲刺速度51 vs 实际冲刺速度48。
第八趴:可视化公式
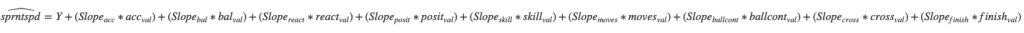
我们需要再次看下我们的多元线性方程来可视化我们的预测公式。
简单来说,预测值是关于每个预测因子的斜率与他们的值的乘积的函数(比如加速度是80,我们把加速度的斜率与80相乘),我们把这些加在一起并且把总共的数字加到y轴的截距。

我们可以用.coef_ 函数来得到每个因子的系数或斜率。
我们之后可以用接下来的Python代码来解读这个等式。

运用这个公式,我们可以把josef_stats 列表里的每个值和它对应的斜率相乘,把他们相加然后加上我们用model.intercept_函数得到的截距,得出预测的冲刺速度51。
原文作者:Emmanuel Sibanda
翻译作者:Manxi
美工编辑:Miya
校对审稿:卡里


