
使用Python的scikit-learn进行特征缩放
归一化的主要目标之一是使数据接近零。这使得优化问题更加“数值稳定”。
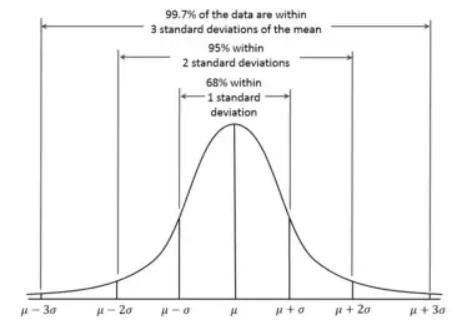
现在,使用均值和标准偏差的缩放比例假定数据是正态分布的,也就是说,大多数数据都足够接近均值。因此,将均值移到零可确保大多数数据点的大多数分量都接近于0。具体来说,从下图可以看出,68%的数据将在-1和1之间:
在本文中,我们探讨了scikit-learn中实现的3种特征缩放方法:
· StandardScaler
· MinMaxScaler
· RobustScaler
· Normalizer
标准缩放(Standard Scaler)
StandardScaler假定你的数据正态分布在每个要素中,并将对其进行缩放,以使分布现在以0为中心,标准偏差为1。
计算特征的平均值和标准偏差,然后根据以下条件对特征进行缩放:
如果数据不是正态分布的,那么这不算是最佳的缩放方法。
让我们来看看它的实际操作:
In [1]:
import pandas as pd
import numpy as np
from sklearn import preprocessing
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
matplotlib.style.use(‘ggplot’)
In [2]:
np.random.seed(1)
df = pd.DataFrame({
‘x1’: np.random.normal(0, 2, 10000),
‘x2’: np.random.normal(5, 3, 10000),
‘x3’: np.random.normal(-5, 5, 10000)
})scaler = preprocessing.StandardScaler()
scaled_df = scaler.fit_transform(df)
scaled_df
= pd.DataFrame(scaled_df, columns=[‘x1’, ‘x2’, ‘x3’])fig, (ax1, ax2) =
plt.subplots(ncols=2, figsize=(6, 5))ax1.set_title(‘Before Scaling’)
sns.kdeplot(df[‘x1’], ax=ax1)
sns.kdeplot(df[‘x2’], ax=ax1)
sns.kdeplot(df[‘x3’], ax=ax1)
ax2.set_title(‘After Standard Scaler’)
sns.kdeplot(scaled_df[‘x1’], ax=ax2)
sns.kdeplot(scaled_df[‘x2’], ax=ax2)
sns.kdeplot(scaled_df[‘x3’], ax=ax2)
plt.show()
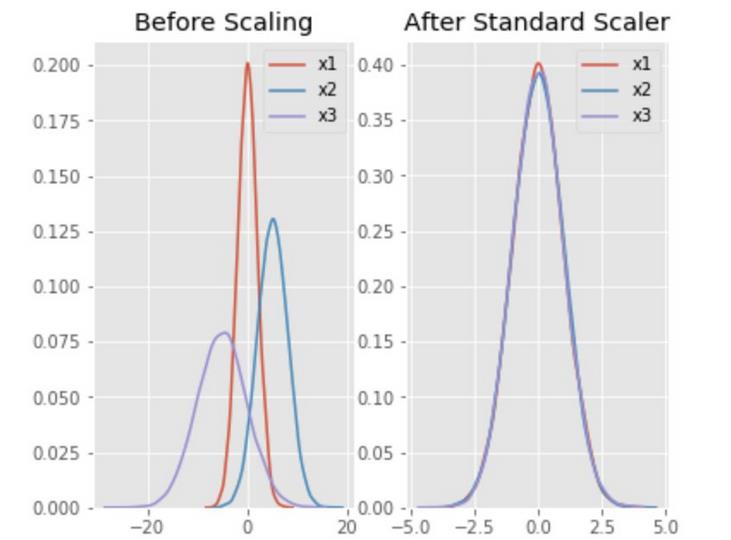
现在所有的特征都缩放至了相似的范围。
最大最小值缩放(Min-Max Scaler)
MinMaxScaler可能是最出名的缩放算法,并且针对每个特征遵循以下公式:
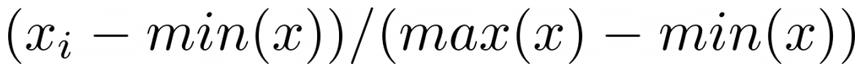
它会缩小范围,以使该范围现在介于0和1之间(如果存在负值,则为-1到1)。
这个缩放器在标准缩放器可能无法工作的情况下效果更好。如果数据分布不是高斯分布或标准偏差很小,则最小-最大缩放器会更好。
但是,它对异常值很敏感,因此,如果数据中存在异常值,则可能需要考虑下面的RobustScaler。
现在,让我们来看一下最小-最大缩放器的实际操作:
In [3]:
df = pd.DataFrame({
# positive skew
‘x1’: np.random.chisquare(8, 1000),
# negative skew
‘x2’: np.random.beta(8, 2, 1000) * 40,
# no skew
‘x3’: np.random.normal(50, 3, 1000)
})scaler = preprocessing.MinMaxScaler()
scaled_df = scaler.fit_transform(df)
scaled_df = pd.DataFrame(scaled_df, columns=[‘x1’, ‘x2’, ‘x3’])fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(6, 5))
ax1.set_title(‘Before Scaling’)
sns.kdeplot(df[‘x1’], ax=ax1)
sns.kdeplot(df[‘x2’], ax=ax1)
sns.kdeplot(df[‘x3’], ax=ax1)
ax2.set_title(‘After Min-Max Scaling’)
sns.kdeplot(scaled_df[‘x1’], ax=ax2)
sns.kdeplot(scaled_df[‘x2’], ax=ax2)
sns.kdeplot(scaled_df[‘x3’], ax=ax2)
plt.show()
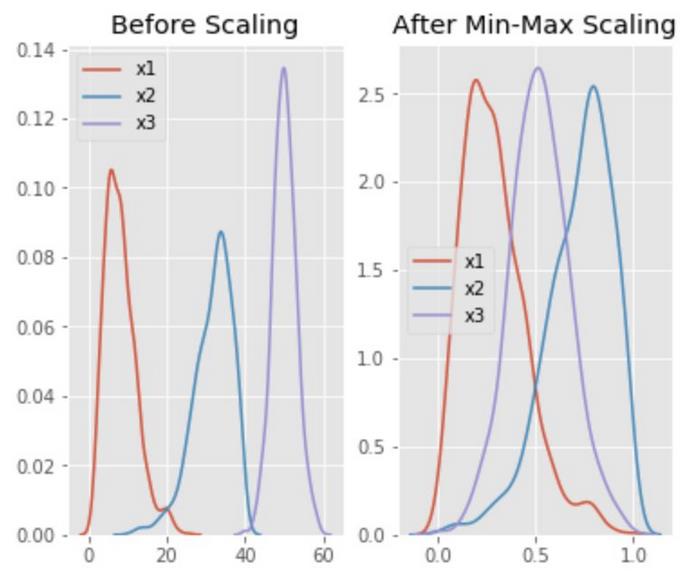
分布的偏度得以保持,但是3个分布现在处于相同的比例,因此它们有所重叠。
稳健缩放 (Roburst Scaler)
RobustScaler使用与最大最小值缩放类似的方法,但它使用四分位间距而不是最大值和最小值,因此它对异常值具有鲁棒性。它遵循以下公式:
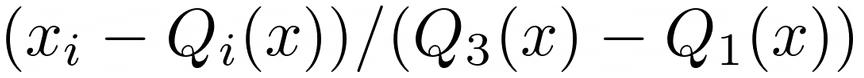
当然,这意味着它使用较少的数据进行缩放,因此更适合数据中存在异常值的情况。
让我们来看看这个在异常数据上的实际操作
In [4]:
x = pd.DataFrame({
# Distribution with lower outliers
‘x1’: np.concatenate([np.random.normal(20, 1, 1000), np.random.normal(1, 1, 25)]),
# Distribution with higher outliers
‘x2’: np.concatenate([np.random.normal(30, 1, 1000), np.random.normal(50, 1, 25)]),
})scaler = preprocessing.RobustScaler()
robust_scaled_df = scaler.fit_transform(x)
robust_scaled_df = pd.DataFrame(robust_scaled_df, columns=[‘x1’, ‘x2’])scaler = preprocessing.MinMaxScaler()
minmax_scaled_df = scaler.fit_transform(x)
minmax_scaled_df
= pd.DataFrame(minmax_scaled_df, columns=[‘x1’, ‘x2’])fig, (ax1, ax2,
ax3) = plt.subplots(ncols=3, figsize=(9, 5))
ax1.set_title(‘Before Scaling’)
sns.kdeplot(x[‘x1’], ax=ax1)
sns.kdeplot(x[‘x2’], ax=ax1)
ax2.set_title(‘After Robust Scaling’)
sns.kdeplot(robust_scaled_df[‘x1’], ax=ax2)
sns.kdeplot(robust_scaled_df[‘x2’], ax=ax2)
ax3.set_title(‘After Min-Max Scaling’)
sns.kdeplot(minmax_scaled_df[‘x1’], ax=ax3)
sns.kdeplot(minmax_scaled_df[‘x2’], ax=ax3)
plt.show()
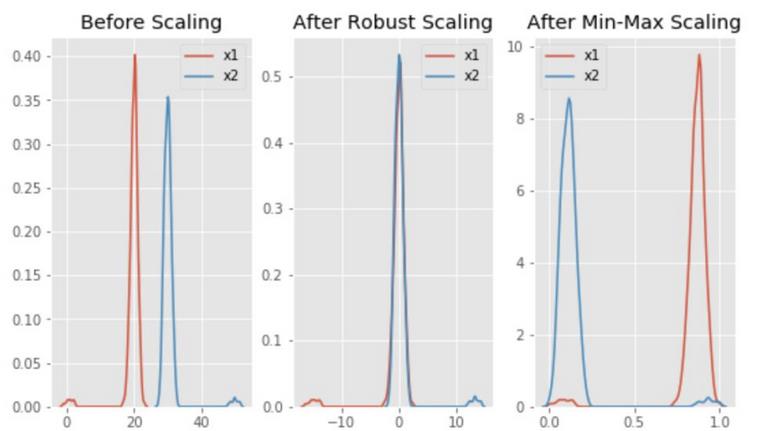
请注意,经过稳健缩放后,这些分布被带入相同的比例并重叠,但离群值仍在新分布的主体之外。
但是,在最大最小值缩放中,两个正态分布被位于0-1范围内的离群值分开。
归一化(Normalizer)
归一化缩放通过对nn个特征的nn维空间中的每个值除以其大小来缩放每个值。
假设你的特征是x,y和z笛卡尔坐标,则x的缩放比例值为:
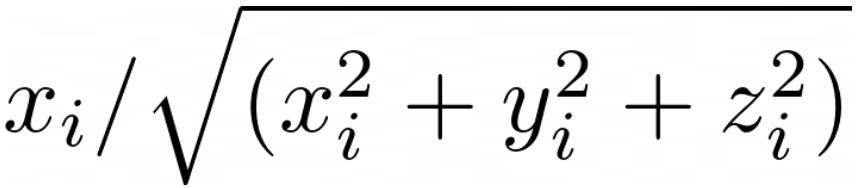
现在,每个点都在此笛卡尔坐标系上距离原点1单位以内。
In [5]:
from mpl_toolkits.mplot3d import Axes3Ddf = pd.DataFrame({
‘x1’: np.random.randint(-100, 100, 1000).astype(float),
‘y1’: np.random.randint(-80, 80, 1000).astype(float),
‘z1’: np.random.randint(-150, 150, 1000).astype(float),
})scaler = preprocessing.Normalizer()
scaled_df = scaler.fit_transform(df)
scaled_df = pd.DataFrame(scaled_df, columns=df.columns)fig = plt.figure(figsize=(9, 5))
ax1 = fig.add_subplot(121, projection=’3d’)
ax2 = fig.add_subplot(122, projection=’3d’)
ax1.scatter(df[‘x1’], df[‘y1’], df[‘z1’])
ax2.scatter(scaled_df[‘x1’], scaled_df[‘y1’], scaled_df[‘z1’])
plt.show()
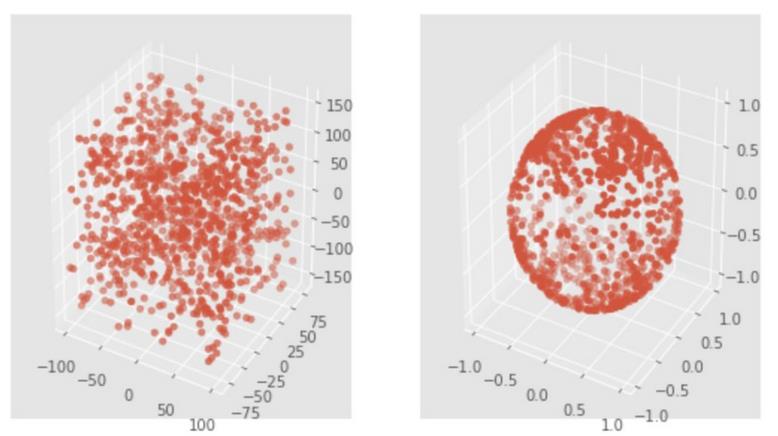
所有点都被带到一个球体中,该球体在任何点都距原点最多1个距离。 同样,以前不同比例的轴现在都是一个比例。





