
关于线性回归:一个关键且经常被误解的事实
关于线性回归,如果你必须要了解什么的话,那就是——
线性回归是统计学和机器学习中方法最简单的建模技术之一。这有好有坏。如果你想了解更多关于统计的相关内容,可以阅读以下这些文章:
数据科学家须知:统计学中的5个悖论
数据/商业分析师求职,如何准备统计相关面试题?
数据科学家,知道这些统计知识就对了
数据科学家八大最常见统计面试题
为什么说这是一件好事?因为在许多建模情况下,线性回归做得足够好,可以让我们避免更复杂、更难以解释的技术。为什么又说这是一件坏事呢?因为它“表面的”简单性导致许多人在完全不了解其运作原理的情况下就仓促地开始了使用。
据我所见,线性回归最常被滥用在其“基础假设”技术上。线性回归只在数据假设很难推测的情况下起作用,如果这些假设是错误的,那么你作为解释器或预测器的模型可能并没有什么用。
在这篇文章中,我想谈谈线性回归最重要的假设之一:残差正态性假设。如果你没有正确地理解这个假设,那么你可能会犯一些非常严重的错误,例如:
- 为你的数据拟合错误的模型,导致出现显著性和效应量的错误结论
- 对模型拟合和误差区间给出了极不准确的解释
- 意识不到你可能需要考虑其他模型类型
下面我将告诉你如何一步一步地在进行线性回归建模时很好地使用这个重要的假设。
归纳偏置——残差正态分布
当你决定使用线性回归模型对一组数据进行建模,也就是说,你在使用归纳偏置。也许你以前从没有听过这个词:它用来描述一个事实,即任何建模实践都含有人为决策。人们会决策模型类型的选择,在某些情况下,还会决策输入参数的选择。
当你选择使用线性回归时,你就是在做人为决策——你猜测这可能是一个很好的数据模型。而这,即是你的归纳偏置。就像所有人在做决定时会犯错一样,你也逃不过这个事实。
当建模者不对他们的归纳偏置进行数据真实性调查时,他们就很可能会犯最大的建模错误——而且他们基本上接受了结果后,无论发生什么都跟着结果走。很不幸,这种行为非常普遍。
归纳偏置会出现一个结果:在线性回归的情况下,你会对你的数据假设出某种非常特定的形状。让我们看一些基础数学原理,于此我们可以考虑进行简单的线性回归,让事情简单化(原理很容易概括为多元线性回归)。
简单线性回归,假设输入(因变量)x和结果(自变量)y的平均值之间存在线性关系。对输入变量x_i进行相同的特定观察,并对其多次采样,我们预计结果变量μ(y_i)的平均值将沿着直线下降:
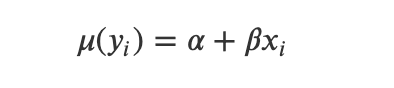
但正如我们所知,许多抽样观测值的平均值并不等于单个观测值,y_i的任何单个观测值都会与这个平均值相比有所偏差,所以:
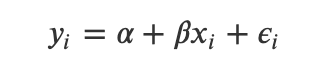
某些值,即ε_i会被称为误差项或残差。当然,对于x_i的众多观测值,我们希望μ(ε_i)=0,以便与我们的第一个方程一致。这就是经常被遗忘的额外假设:
我们的残差ε_i被假设在平均值为0附近具有正态分布。
为什么需要这个额外的假设?其实这是必要的,为了使用最小二乘法估计模型的系数,并确定这些系数的置信区间,我们需要知道我们正在处理的就是正态分布的残差。如果没有这个假设,我们的方法就不能依赖于高斯统计基础设施,从而无法使用线性回归所依赖的普通最小二乘法(OLS)进行最优估计。
为了更直观地理解这一假设,请看一下我创建的这个3D图表。该图基于平均值周围的个体观测结果呈正态分布(z轴)的假设,显示了输入变量和结果变量的平均值(x轴和y轴)之间的近似线性关系。线性回归就是为这样的数据而设计的。
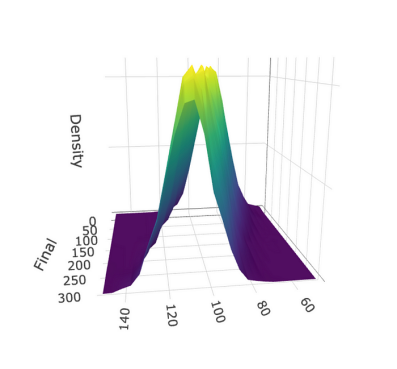
被许多人误解的另一个重要的点是,线性回归模型预测的置信区间实际上是许多样本(基本上是图中的黄色区域)的平均预测区间。这不是一个单个预测的区间,它代表了整个图表的95%。特定预测的区间被称为预测区间,比置信区间宽得多。
数学原理够了——这在实践中到底意味着什么?
让我们举一个例子(数据集是在线的,所以如果你愿意,可以使用我的代码)。
我将使用一个名为“毕业生”的数据集,其中包含美国各个教育学科大学毕业生的就业信息。
url <- "https://peopleanalytics-regression-book.org/data/graduates.csv"graduates <- read.csv(url)我们来看看此数据集的四列:
- Discipline是大学学位的学科
- Total是美国某一特定学科的毕业生总数
- Unemployment_rate是该学科目前的失业率
- Median_salary是该学科当前的中值薪水
在这四列的基础上,我们来看看前几个值:
graduates <- subset(graduates, select = c("Discipline", "Total", "Unemployment_rate", "Median_salary"))head(graduates)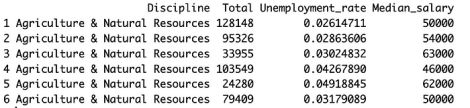
现在,让我们继续我们的归纳偏置:线性回归模型将把Median_salary作为结果变量与Discipline、Total和Unemployment_rate作为输入变量联系起来。因此,我们假设:
- 平均来说,工资中位数与学科、失业率和毕业生总数呈线性相关
- 残差呈正态分布
现在,让我们运行一个多元回归模型,看看它是怎么做的。我将把失业率乘以100,以了解它在百分点范围内的影响:
graduates$Unemployment_rate <- 100*graduates$Unemployment_ratemodel <- lm(
formula = Median_salary ~ .,
data = graduates
)summary(model)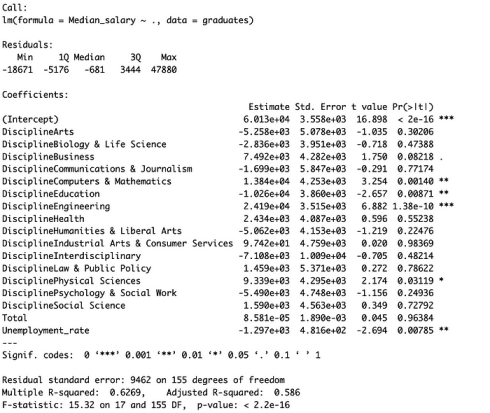
我们看到失业率与中值薪水有显著的负相关,某些学科有显著的正相关或负相关。我们的R平方约为0.6,这表示了拟合是适度的。事实可能比我们所得到的答案更好。
做到这儿,许多人会宣布“完成”了,并开始运行他们的模型。但是,我们是否考虑过:我们的归纳偏置适合这个数据集吗?
我们的残差是正态分布的吗?
让我们画出残差图,看看它们的分布情况。
plot(density(model$residuals))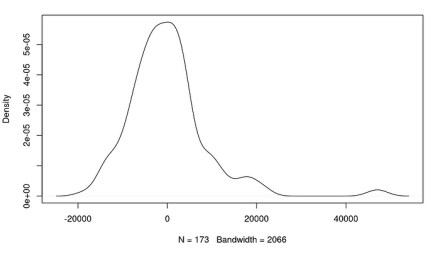
好吧,这是一个相当倾斜的分布情况——似乎有一个异常高的残差影响着这个模型。我们还可以做一个分位数散布图,直接将我们模型的剩余分位数与理论正态分布的预期分位数进行比较。
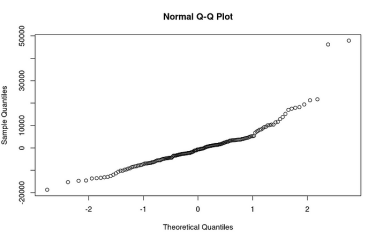
看到上角的那两个数据点了吗?他们似乎基本上“逃脱”了这个分布。
怎么办呢?
在这种情况下,你的模型还能救回来。我们把这两个异常值丢弃,重新运行模型,我们会看到更正态的残差分布。如果你调查一下,你会发现这两个异常值与石油工程和制药管理专业有关。如果你的用例允许丢掉这两个学科,重新运行模型后,你将看到一个更“健康”的残差分布,它与你的归纳偏置更加一致:
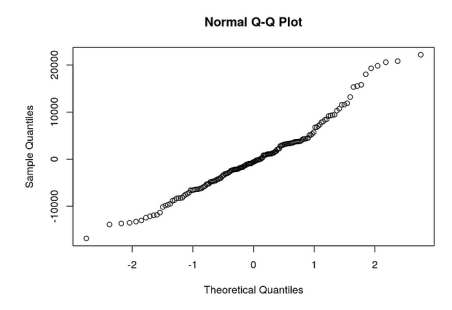
由于你的数据和归纳偏置之间更加一致,你的模型拟合度会提高(你的R平方现在将接近0.7),你对参数的估计也会更可靠——事实上,跳出这个用例,你的预测一样会更准确(当然,假设你将来不在石油或制药领域进行建模)。
你还可以选择不同的模型,从而改变你的归纳偏置。现有的各种L2正则化方法(如Huber回归)都可以降低异常残差的影响。
如果你觉得这很有用,可以点击这里:https://peopleanalytics-regression-book.org/看看我对回归方法的理解——请随时在评论中分享你的观点。
感谢阅读。你还可以订阅我们的YouTube频道,观看大量大数据行业相关公开课:https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ;在LinkedIn上关注我们,扩展你的人际网络!https://www.linkedin.com/company/dataapplab/
原文作者:Keith McNulty
翻译作者:高佑兮
美工编辑:过儿
校对审稿:Chuang
原文链接:https://keith-mcnulty.medium.com/a-critical-and-often-misunderstood-fact-about-linear-regression-d2214207cbb4





