
数据科学家,知道这些统计知识就对了
在这个数据驱动的世界中,我们都认识到统计学给数据科学领域带来了巨大影响。数据科学中,最重要的步骤是发现模式、趋势并进行预测。
本篇文章将讨论统计领域的一些基本术语,这些术语在统计数据分析中起着至关重要的作用。如果你想了解更多数据分析相关内容,可以阅读以下这些文章:
Sampling 101:详解统计学中的抽样技术
AB 测试应用:AB Testing在社交领域的实践及挑战
数据科学家八大最常见统计面试题
长文总结在机器学习中处理倾斜数据集

数据类型和数据中的个体
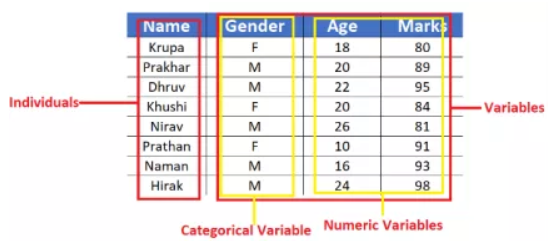
- 单位:单位是研究中包含的人或物体。数据所描述的内容就是单位。在这样的表格中,一行表示一个单位,它们也被称为标识符。
- 变量:变量描述了通过测量获得的个体信息,如长度、时间、直径、强度、重量、温度、密度、厚度、压力和高度。你可以用这些变量轻松获取个人或群体的趋势。
数据类型主要分为以下两种:
- 数字数据:这类数据用数字表示并且是可测量的。该数据可进一步分为离散数据或连续数据两个子类别,例如身高、速度、年龄、体重、销售额、成本等。
- 分类数据:即分成组的信息的集合。定性数据分为几类,即性别、年龄组、产品类别、教育水平等。
- 均值:即数据集的数学平均值。
- 中位数:即按升序或降序排序的数字列表中的中间数字,比平均值更能说明该数据集。
- 众数:即一组数据中最常看到的值。
变量的衡量
- 范围:即数据集中最高值和最低值之间的差值。
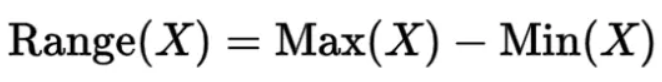
其中,X为数据集,
方差(σ^2):用来衡量数据集的分散程度。
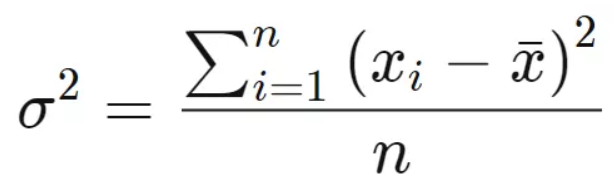
标准差(σ):用来衡量一组数据与其均值的离散程度。
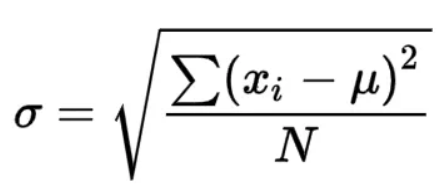
Z 分数:Z 分数是一种数据化计量,用于描述一个值与一组值的均值之间的关系。 Z 分数是根据与平均值的标准偏差来衡量的。
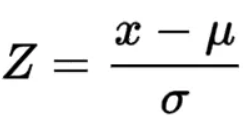
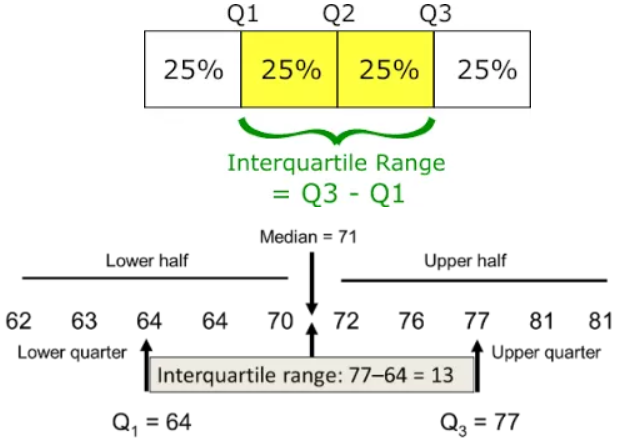
IQR(四分位距):四分位距是衡量“中间百分之五十”在数据集中的位置。
平均绝对偏差(MAD)
数据集的平均绝对偏差,是每个数据点与平均值之间的平均距离。我们可以通过平均绝对偏差了解数据集的可变性。
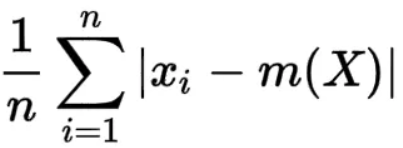
其中,
n=数据值的数量
xi=数据集中的数据值
m(x)=数据集平均值
峰度和偏度
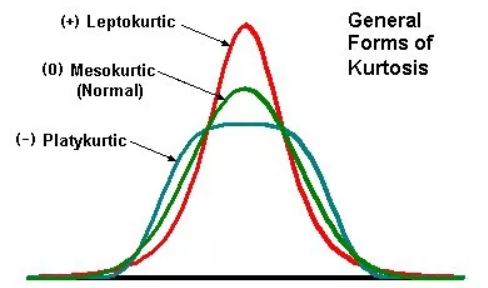
峰度(Kurtosis):特点为平坦或尖峭,用来衡量数据在正态分布中是重尾还是轻尾。
- 中峰 (Mesokurtic):分布宽度适中,曲线峰高中等。
- 低峰 (platykurtic):尾部的值越少,接近均值的值越少。(即曲线有一个平坦的峰值)
- 高峰(leptokurtic) :分布尾部的更多值和更多接近均值的值(即尖峰与重尾)
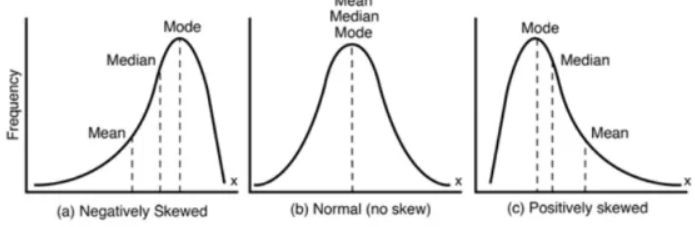
- 偏度:偏度用来衡量分布对称性。如果模式一侧的尾部比另一侧更粗或更长,则分布是偏斜的,即不对称的。
- 正偏(Positively skewed):表示右侧的尾巴比左侧的长。
- 负偏斜(Negatively skewed):表示左边的尾巴比右边的长。
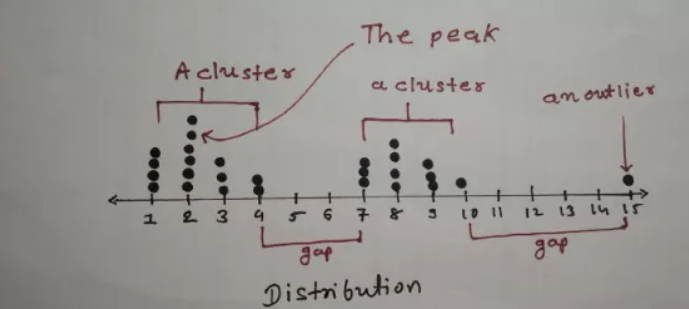
- 集群(Cluster):即区分于其他组,并聚集起来的一组值。
- 异常值(Outliers):区分于大多数(多数值)的少数值。
异常值并不影响中位数和众数,只影响分布的方法。
- 峰值(Peaks):分布中的最大值。
- 间隙(Gaps):某些数据点之间的“大型”开放空间。
变量之间关系的测量:
协方差:
协方差决定了两个随机变量或样本之间的关系——它们是如何一起变化的。或者换句话说,也可以说协方差是衡量两个随机变量一起波动的程度。
协方差可以计算为,
1. 总体协方差公式。
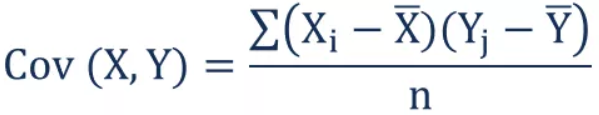
2. 样本协方差公式。
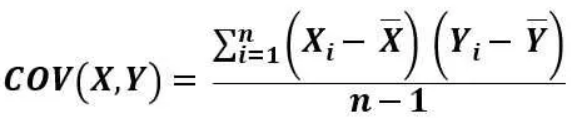
相关性:
相关性是一种统计学度量,表明两个变量线性相关的强度。或者说,相关性是一种统计学度量,表示两个或多个变量一起波动的程度。
相关性可以计算为,
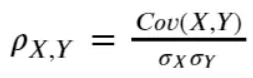
矩(Moments)
矩描述了分布的性质和形状的不同方面。第一个矩是均值,第二个矩是方差,第三个矩是偏度,第四个矩是峰度。

感谢阅读!你还可以订阅我们的YouTube频道,观看大量数据科学相关公开课:https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ;在LinkedIn上关注我们,扩展你的人际网络!https://www.linkedin.com/company/dataapplab/
原文作者:Prakhar Patel
翻译作者:Lia
美工编辑:过儿
校对审稿:Jiawei Tong
原文链接:https://patel-prakhar09.medium.com/basic-fundamentals-of-statistics-every-data-scientist-should-know-ab30425c6f76





