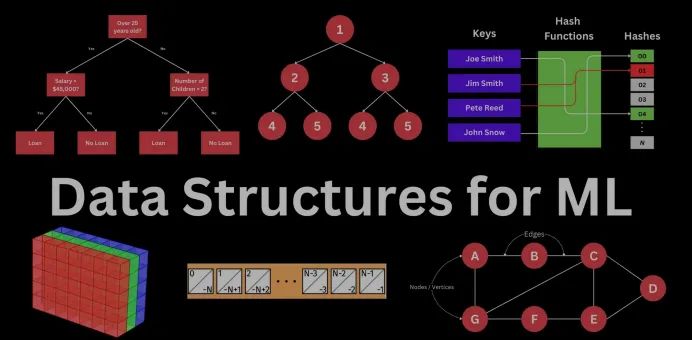
机器学习工程师和数据科学家必须了解的5种数据结构(一)
在机器学习中,模型的性能和可扩展性通常依赖于所选的数据结构。无论是组织大型数据集、管理复杂关系,还是优化算法效率,合适的数据结构会带来显著影响。
数组、堆、哈希表、树和图——这些理论概念和实用工具——可以帮助模型运行得更快、占用更少的内存,并处理更复杂的任务。
本文将介绍这五种核心数据结构,揭示它们在各种机器学习应用中的关键作用,以及如何提升你的建模能力。如果你想了解更多关于机器学习的相关内容,可以阅读以下这些文章:
金融中的机器学习:利用随机森林掌握时间序列分类
每个机器学习工程师都应该知道的线性代数!!
2023年面向开发者的十大机器学习(ML)工具
CPU与GPU:哪个更适合机器学习,为什么?
数组和矩阵
数组和矩阵是计算机科学与机器学习中最基本的数据结构之一。数组是存储在连续内存块中的一组元素,通常这些元素具有相同的数据类型。数组是索引的,这意味着每个元素可以通过其索引(即在数组中的位置)访问。
矩阵是一个二维数组,数据以行和列的形式排列。在机器学习中,特别是在处理表格数据、图像或多维数据时,矩阵是不可或缺的。数组表示一维向量(即一维数据),而矩阵表示更复杂的二维关系,在多种场景中具有非常重要的作用。
数学符号表示法:
一个具有m行和n列的矩阵A可以表示为:

机器学习中的应用
1.数据表示(特征向量、图像):
特征向量:在机器学习中,我们常常将数据表示为向量。例如,我们可以用n维向量描述一个具有n个特征(变量)的数据集:
其中,每个xᵢ是一个特征值。
在Python中索引大小为N的特征向量的示例视图(参见下图)。
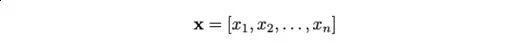
大小为n的数组(或特征向量)。请注意,在Python中,索引从0开始,负索引从列表末尾到作者创建的开始图像计数。
给定m个样本向量,让我们将它们组合成一个大小为m×n的矩阵X,其中每行代表一个样本。

图像:在计算机视觉中,图像通常表示为矩阵,每个元素对应一个像素值。对于灰度图像,每个元素表示一个强度值。而彩色图像的每个像素由三个值表示,例如RGB值,如下图所示。
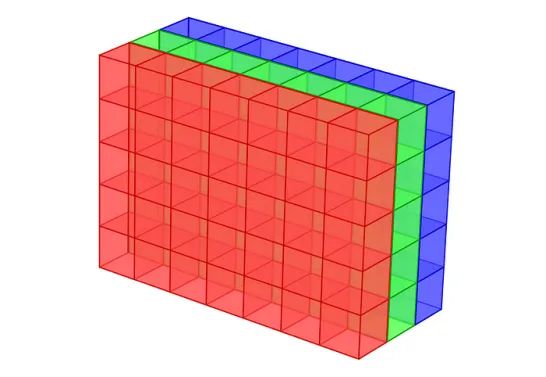
我们可以表示大小为28×28的灰度图像如下。
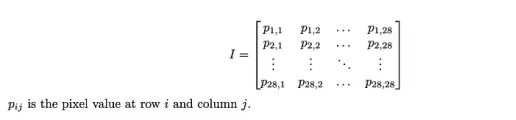
2. 线性代数中的矩阵运算:
矩阵也是机器学习中许多操作的核心,特别是在线性代数中,这是该领域的基础。
矩阵乘法:这是机器学习中最常见的操作之一。给定一个m×n的矩阵A和一个n×p的矩阵B,它们的乘积C是一个m×p的矩阵:
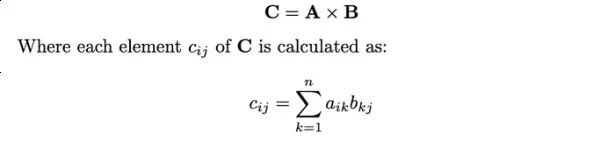
这个操作在神经网络中是至关重要的,我们将权重和输入数据表示为矩阵,它们的乘积是层操作的基础。
线性回归的示例:在线性回归中,目标是找到一个系数向量β,使得预测值和目标值之间的差异最小化。这个模型可以表示为:

为了估计β,我们使用正态方程。
Python实现示例
import numpy as np
# Example dataset
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]]) # Feature matrix
y = np.dot(X, np.array([1, 2])) + 3 # Target vector
# Add a column of ones to X to account for the intercept term
X = np.hstack([np.ones((X.shape[0], 1)), X])
# Calculate beta using the normal equation
beta = np.linalg.inv(X.T @ X) @ X.T @ y
print("Estimated coefficients:", beta)这些系数分别对应于特征的截距和斜率。
效率考量
基本操作的时间复杂度:
- 访问:在数组或矩阵中访问一个元素是O(1)操作,因为我们可以直接通过索引访问每个元素。
- 遍历:遍历一维数组的时间复杂度为O(n),遍历具有m行n列的矩阵的时间复杂度为O(m×n)。
- 矩阵乘法:两个矩阵相乘的时间复杂度为O(m×n×p)。
内存使用及潜在优化:
内存使用:数组和矩阵在处理大规模或高维数据时可能会占用大量内存。例如,一个10000×10000的矩阵需要存储1亿个元素,可能会占用大量内存,具体取决于数据类型。
稀疏矩阵:如果矩阵包含大量的零值(稀疏矩阵),仅存储非零元素会更节省内存。Python库如scipy.sparse提供了处理稀疏矩阵的方法。
from scipy.sparse import csr_matrix
# Create a sparse matrix
dense_matrix = np.array([[0, 0, 3], [4, 0, 0], [0, 2, 0]])
sparse_matrix = csr_matrix(dense_matrix)
print(sparse_matrix)
(0, 2) 3
(1, 0) 4
(2, 1) 2批处理:按批次进行操作而非一次处理整个数据集,可以减少内存负担,缩短大规模数据处理的时间。
数据类型优化:选择适当的数据类型(例如,使用float32而不是float64)可以减少内存占用,同时为许多应用程序保持足够的精度。
总之,数组和矩阵是机器学习中数据表示和操作的基石。理解它们的应用、运算及效率考量对于开发高效且可扩展的机器学习模型至关重要。
堆
堆是一种特殊的树形数据结构,具有堆属性。在最大堆中,任何给定节点i的值大于或等于其子节点的值;而在最小堆中,节点i的值小于或等于其子节点的值。这一属性确保了根节点始终包含最大(最大堆)或最小(最小堆)的元素,使得堆非常适合实现优先队列。
堆通常实现为二叉树,其中每个父节点最多有两个子节点。堆的结构可以用数组表示,通过对索引进行简单的算术运算来方便地管理父子节点关系。
Max-Heap属性:
对于max-heap,每个节点的值大于或等于它的子节点的值:
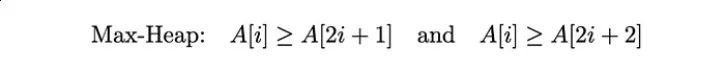
最小堆属性:
对于最小堆,每个节点的值小于或等于它的子节点的值:
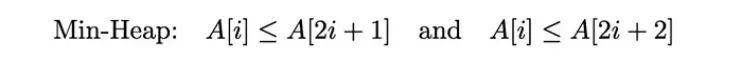
机器学习中的应用
算法中的优先队列(如A*搜索): 在AI规划和路径搜索算法(如A*)中,堆被用来高效地实现优先队列。优先队列根据元素的优先级进行排序,允许算法不断扩展最有前景的节点。最小堆通常用于此类场景,其中具有最低成本的节点位于根节点,可以持续访问。
import heapq
# Example graph (as an adjacency list)
graph = {
'A': [('B', 1), ('C', 4)],
'B': [('A', 1), ('C', 2), ('D', 5)],
'C': [('A', 4), ('B', 2), ('D', 1)],
'D': [('B', 5), ('C', 1)]
}
# A* search function
def a_star(graph, start, goal, h):
# Priority queue, initialized with the start node
pq = [(0 + h(start), 0, start, [])] # (f = g + h, g, node, path)
heapq.heapify(pq)
while pq:
(f, g, current, path) = heapq.heappop(pq)
# Path to the current node
path = path + [current]
if current == goal:
return path, f # Return the found path and its total cost
for (neighbor, cost) in graph[current]:
heapq.heappush(pq, (g + cost + h(neighbor), g + cost, neighbor, path))
return None # If no path is found
# Heuristic function (for simplicity, using zero heuristic as an example)
def h(node):
return 0
# Find path from A to D
path, cost = a_star(graph, 'A', 'D', h)
print("Path:", path, "Cost:", cost)
Path: ['A', 'B', 'C', 'D'] Cost: 4示例:使用最小堆进行A*搜索。
在本例中,最小堆存储了A*搜索算法的节点各自的开销(优先级)。堆确保首先扩展成本最低的节点,从而优化搜索过程。
2.聚类算法中的大规模数据管理(如K-means): 在K-means等聚类算法中,堆可用于高效管理和更新质心。特别是在处理大量数据点时,堆有助于优化选择和更新质心的过程,确保高效计算最近的质心。
示例:使用堆进行K-means初始化(k -means++)
k -means++是一种初始化技术,它选择初始质心来加速收敛。堆可以有效地管理点到最近质心的距离。
import numpy as np
def initialize_centroids(X, k):
centroids = []
centroids.append(X[np.random.randint(X.shape[0])])
for _ in range(1, k):
distances = np.array([min([np.linalg.norm(x - c) for c in centroids]) for x in X])
heap = [(dist, i) for i, dist in enumerate(distances)]
heapq.heapify(heap)
# Weighted random selection of the next centroid
total_dist = sum(distances)
r = np.random.uniform(0, total_dist)
cumulative_dist = 0
for dist, i in heap:
cumulative_dist += dist
if cumulative_dist >= r:
centroids.append(X[i])
break
return np.array(centroids)
# Example dataset
X = np.array([[1, 2], [1, 4], [3, 2], [5, 6], [7, 8], [9, 10]])
centroids = initialize_centroids(X, 2)
print("Initial centroids:\n", centroids)
Initial centroids:
[[ 9 10]
[ 5 6]]这里,我们在k- meme++中初始化质心期间使用堆来管理数据点到最近质心的距离。这确保了质心被选择为最大化它们之间的最小距离,从而获得更好的聚类结果。
效率考量
插入与删除操作的对数时间复杂度:
- 插入:向堆中插入一个元素的时间复杂度为O(log n),因为可能需要移动元素以保持堆的属性。
- 删除:删除根节点(最大堆中的最大值或最小堆中的最小值)的时间复杂度为O(log n)。删除后需要重构堆以维持其属性。
由于这些复杂性,堆在需要频繁访问最高或最低优先级元素的场景中非常高效,如优先队列或机器学习中的动态数据集管理。
空间复杂度:
- 堆的空间复杂度为O(n),n是堆中元素的数量。堆通常通过数组实现,不需要额外的指针,因此更加节省空间。
总之,堆是一种强大的数据结构,特别适用于机器学习中的优先级操作和大规模数据管理。其对数时间复杂度使其在实时系统和大规模机器学习任务中表现优异。
哈希表
哈希表是一种实现关联数组的数据结构,这种结构可以将键映射到值。它基于键值对的概念,每个键都是唯一的,并与特定的值相关联。由于其能够快速进行数据检索、插入和删除操作,哈希表在计算中被广泛使用。
哈希表的效率来自于哈希函数,它接受一个键并计算出数组中的索引(哈希码,通常称为哈希表)。然后,键值对存储在由哈希码指示的位置。当需要检索值时,对该键应用相同的哈希函数,计算出的索引能快速定位到相应的值。
哈希函数:
一个好的哈希函数应具备以下特性:
- 哈希码应均匀分布,尽量减少多个键映射到相同索引(即碰撞)的几率。
- 哈希函数应具有确定性,即同一个键每次都会产生相同的哈希码。
数学表示法:
给定一个键k和哈希函数h,键值对在哈希表中的位置索引i由以下公式表示:
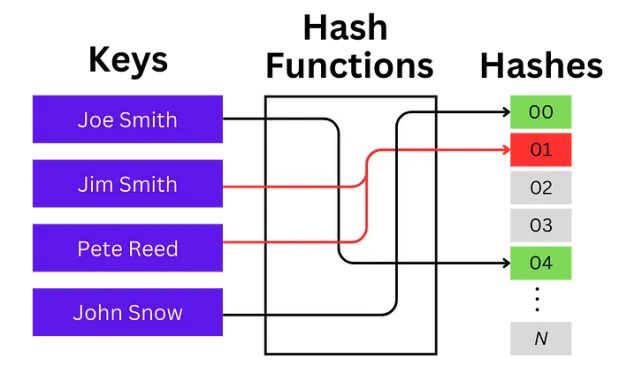
哈希函数运作示例:
不同的键(例如姓名)通过哈希函数生成唯一的哈希值。当多个键映射到相同的哈希值时(如“Jim Smith”和“Pete Reed”映射到哈希值‘01’),就会发生碰撞,这突显了哈希表中需要碰撞解决策略。
机器学习中的应用
大数据集的高效查找: 哈希表在需要高效从大规模数据集中检索数据时非常有用。例如,在一个包含用户交互(如点击、浏览、购买)的数据集中,哈希表可以快速访问与特定用户相关的交互信息。
# Example dataset: user interactions with items
user_interactions = {
'user1': ['item1', 'item2', 'item3'],
'user2': ['item2', 'item4'],
'user3': ['item1', 'item4', 'item5'],
}
# Hash table (dictionary in Python) to store interactions
hash_table = {}
# Insert interactions into the hash table
for user, items in user_interactions.items():
hash_table[user] = items
# Efficient lookup of a user's interactions
user = 'user2'
print(f"Items interacted with by {user}: {hash_table[user]}")
Items interacted with by user2: ['item2', 'item4']示例:高效查找
在这个示例中,即使数据集包含数百万用户,哈希表也能以恒定时间快速检索特定用户的交互记录。
2.近似最近邻搜索中的哈希技术(如局部敏感哈希LSH): 局部敏感哈希(LSH)是一种利用哈希表快速进行高维空间近似最近邻搜索的技术。当数据集过大以至于难以进行精确的最近邻搜索时,它非常有用。LSH通过高概率将相似的输入项映射到相同的“桶”中,显著减少了搜索空间。
import numpy as np
from sklearn.neighbors import NearestNeighbors
from sklearn.random_projection import SparseRandomProjection
# Example dataset: 2D points
points = np.random.rand(1000, 2)
# Using random projections to approximate nearest neighbors
lsh = SparseRandomProjection(n_components=2)
projected_points = lsh.fit_transform(points)
# Using NearestNeighbors for finding approximate neighbors
nbrs = NearestNeighbors(n_neighbors=3, algorithm='ball_tree').fit(projected_points)
distances, indices = nbrs.kneighbors(projected_points)
# Example: Finding nearest neighbors of a point
point_index = 0
print(f"Nearest neighbors of point {point_index}: {indices[point_index]}")
Nearest neighbors of point 0: [ 0 129 312]示例:Python中的LSH
在这个示例中,LSH将高维点投影到低维空间,同时保留它们之间的距离。然后使用类似哈希表的结构快速检索任意点的最近邻。
推荐系统中的哈希表: 在推荐系统中,哈希表可以高效地将用户映射到他们的交互项。这种技术在处理包含数百万用户和物品的大规模系统中至关重要。
示例
考虑一个推荐系统需要快速检索用户已交互的所有物品,以便推荐相似物品。哈希表允许推荐系统快速访问用户评分过的物品,进而生成个性化推荐。
# Example hash table for user-item interactions
recommendation_data = {
'user1': {'item1': 5, 'item2': 3, 'item3': 2},
'user2': {'item2': 4, 'item4': 5},
'user3': {'item1': 2, 'item4': 3, 'item5': 5},
}
# Efficient retrieval of items and their ratings for a specific user
user = 'user3'
items = recommendation_data[user]
print(f"Items and ratings for {user}: {items}")
Items and ratings for user3: {'item1': 2, 'item4': 3, 'item5': 5}在这里,哈希表允许推荐系统快速访问用户已评级的项目,促进个性化推荐的生成。
效率考量
- 查找操作的平均时间复杂度为O(1): 哈希表最显著的优势之一是查找操作的平均时间复杂度为O(1)。这意味着,无论数据集的大小如何,从哈希表中检索一个值的时间都是恒定的。
- 碰撞问题及其处理策略: 当两个不同的键生成相同的哈希码,并被分配到哈希表中的相同索引时,就会发生碰撞。碰撞会降低哈希表的性能,导致查找时间增加。
为解决碰撞问题,可以采用以下几种策略:
- 链地址法:在此方法中,哈希表中的每个索引指向一个链表(或其他数据结构),存储所有被哈希到该索引的键值对。如果发生碰撞,新键值对将附加到该索引的链表中。
hash_table = [[] for _ in range(10)]
def hash_function(key):
return key % 10
def insert(hash_table, key, value):
index = hash_function(key)
hash_table[index].append((key, value))
insert(hash_table, 15, 'value1')
insert(hash_table, 25, 'value2')
print(hash_table)
[[], [], [], [], [], [(15, 'value1'), (25, 'value2')], [], [], [], []]开放寻址法:在发生碰撞时,在哈希表中寻找另一个空槽来存储键值对。常见技术包括:
- 线性探测:依次查找下一个可用的槽位。
- 二次探测:基于二次函数查找可用槽位。
- 双重哈希:使用第二个哈希函数确定寻找下一个可用槽位的步长。
def insert_linear_probing(hash_table, key, value):
index = hash_function(key)
while hash_table[index] is not None:
index = (index + 1) % len(hash_table)
hash_table[index] = (key, value)
hash_table = [None] * 10
insert_linear_probing(hash_table, 15, 'value1')
insert_linear_probing(hash_table, 25, 'value2')
print(hash_table)
[None, None, None, None, None, (15, 'value1'), (25, 'value2'), None, None, None]示例:线性探测
总之,哈希表在机器学习中是高效的数据检索工具,特别是在处理大规模数据集时。由于查找的平均时间复杂度为O(1),哈希表在高性能应用中必不可少。然而,理解和处理碰撞对于保持哈希表的效率至关重要。
树(包括二叉树、决策树和kd树)
树是计算机科学中的一种基础数据结构,广泛应用于机器学习。树是一种层次结构,包含节点(每个节点包含一个值)和零个或多个子节点。树的顶层节点称为根节点,而没有子节点的节点称为叶节点。
在机器学习中,常见的几种树结构各自用于不同的目的:
二叉树:每个节点最多有两个子节点,分别为左子节点和右子节点。二叉树构成了更复杂树结构的基础,如决策树和二叉搜索树。
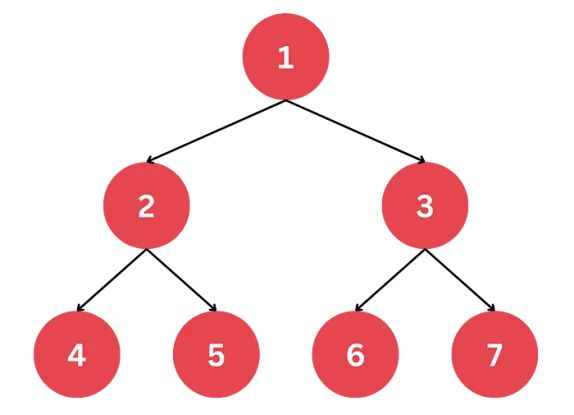
具有7个节点的完整二叉树的可视化表示,展示了一个完美的平衡结构,其中每个级别都是完全填充的,并且所有叶节点都在相同的深度。图片由作者创作。
决策树:决策树是一种树状结构,其中每个内部节点表示基于特征的决策,每个分支表示该决策的结果,每个叶节点表示一个类标签(在分类任务中)或一个连续值(在回归任务中)。
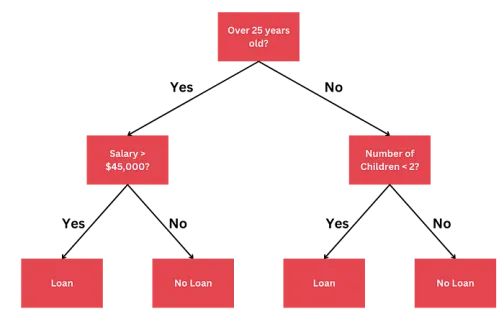
用于确定贷款资格的决策树示例。该树评估如年龄、工资和子女数量等条件,以决定是否批准贷款。
kd树:kd树(即k维树)是一种用于在k维空间中组织点的二叉树。非叶节点充当超平面,将空间分割为两个部分。这在高效的最近邻搜索中非常有用,其目标是找到离查询点最近的点。
为简单起见,如下图所示为k=2的例子。
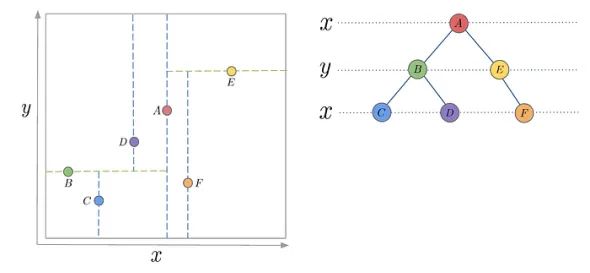
2D kd树及其相应树结构的示例。左图展示了xy平面中A到F点的空间划分,右图则展示了kd树的层次结构,其中每一层交替地沿x轴和y轴进行划分。
第一部分结束。
感谢阅读!你还可以订阅我们的YouTube频道,观看大量大数据行业相关公开课:https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ;在LinkedIn上关注我们,扩展你的人际网络!https://www.linkedin.com/company/dataapplab/。
原文作者:Joseph Robinson, Ph.D.
翻译作者:过儿
美工编辑:过儿
校对审稿:Jason
原文链接:https://pub.towardsai.net/data-structures-in-machine-learning-a-comprehensive-guide-to-efficiency-and-scalability-f7429919c9c5





