Graph ML：图遍历算法简述

当你身处迷宫时，有多种方法可以到达终点。

—— Martellus Bennett

我有一个理论，当你迷失方向时，回到起点，再次尝试迷宫。

——Amanda Seales

广度优先搜索（BFS）和深度优先搜索（DFS）是许多Graph ML算法（如Node2vec、图神经网络等图嵌入技术）的基础。因此，我在这里提供一个简要但完整的介绍，介绍它们是什么、如何工作以及Python实现。在这篇文章中，我只关注与Graph ML相关的信息，以提供对算法工作原理的良好理解（不涉及所有的算法和数据结构课程细节）。

本文内容：

• 图遍历算法的简单介绍
• 如何在Python中实现它们
• 不同方法的优缺点

如果你想了解更多关于算法的相关内容，可以阅读以下这些文章：
利用大型语言模型进行因果推理：为什么知识和算法至关重要？
数据科学算法如何将商业计划变现？
用 K-Means聚类算法(K-Means Clustering)分析客户
数据分析的Regression算法到底是什么？

图遍历算法

图遍历算法被认为是最基本但也是最重要的图算法之一。在设计图算法时，很可能会引入一些图遍历算法。其想法是，从一个顶点s开始，想了解如何到达另一个节点t：找到从一个节点到另一个节点的路径。图遍历对于查找两个节点是否连接以及是否存在最短路径等非常有用。

广度优先搜索（BFS）

BFS是最基本的图遍历算法之一，1959年由Edward F. Moore首次提出，用于寻找走出迷宫的最短路径。BFS还被不同的算法使用，例如最短路径、连通分量搜索和接近中心性的计算。

其想法是，从源节点开始，我们首先探索它的所有直接邻居（一跳距离），然后再移动到其他节点（两跳距离）。这一概念也称为同质性（借用社会学：人们通常与相似的人密切互动），因此相似的节点具有密切的关系。

在BFS中，我们从一个节点s（源节点）开始，开始探索邻居。在一个简单的图中，我们从一个节点开始（图节点顺序是任意的），将其添加到已访问节点列表中，下一个访问的节点将被添加到队列中（存储下一个访问节点的列表）。在接下来的步骤中，我们访问队列中的第一个节点（即节点2），将节点2从队列中移除，并添加它的邻居。该过程持续到队列中的节点访问完毕。

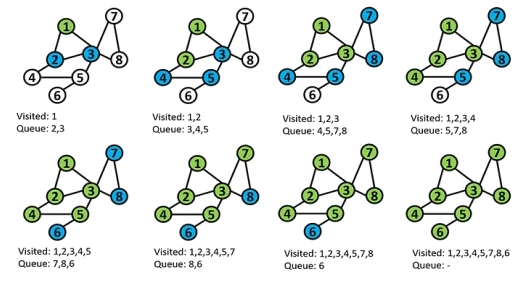
计算时间是O(n+m)，其中n是节点数，m是边数。该算法以线性时间运行，是非常高效的算法。通常，这种算法使用邻接表比使用邻接矩阵计算效率更高。访问节点的顺序通常是邻接表的顺序。

深度优先搜索（DFS）

这个算法由数学家Charles Pierre Trémaux发明，同样用于解决迷宫问题（有趣的是，很多数学家迷失在迷宫中）。

从源节点开始，我们移动到直接邻居（选择一个），然后在回溯之前继续遍历所有路径。与同质性方法相比，这种方法提供了网络中节点的更广泛视角。我们寻找的是节点的结构角色。相似的节点具有所谓的结构等价性。

在这里，我们也从节点s开始，访问节点s的第一个邻居，然后跳到邻居的邻居。其想法是尽可能远离起始顶点。我将访问过的节点列表定义为 Visited，队列表示将要访问的下一个节点。DFS使用堆栈作为存储即将访问节点的结构（即将要访问的下一个节点）。注意，我们从1开始，访问节点2，而不是访问节点3，而是访问节点4。如此反复，直到有一个节点没有未访问的邻居（如节点6）。在这种情况下，我们回溯到前一个顶点。

注意，节点6只有一个邻居，即节点5（但我们已经访问过），所以我们回溯到之前访问的节点6（即节点5）。由于节点5的邻居是节点4和节点3，我们访问节点3，因为节点4已经访问过。

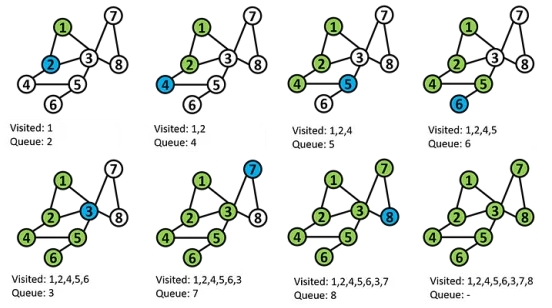
实现方式类似于BFS，计算时间是O(n+m)。注意，DFS仅适用于连通图，从源节点无法到达的节点将不会被列出（尽管存在适用于非连通图的改进版）。

BFS和DFS的应用

BFS用于寻找最小生成树、路径查找、图中环的搜索、对等网络（如torrent）、搜索引擎中的爬虫、社交网络网站、GPS导航系统以及许多其他应用。

BFS用于社交网络，因为它先探索邻居，然后是邻居的邻居，因此如果我们从一个人开始，可能寻找的是朋友或朋友的朋友。另一个例子是，在Facebook上，你希望首先推荐朋友的朋友作为新的潜在联系，而不是网络中的某个人。

DFS算法用于查找顶点之间的路径、检查图中的环、测试图是否为二分图、拓扑排序、解决迷宫和其他难题。DFS在游戏和谜题解决中被使用，因为当我们做出一个决定时，我们会探索从这个决定开始的所有路径（如果这个决定导致获胜，我们就停止）。例如，在棋类或井字游戏中，我们可以将我们的移动想象成对手的移动，我们的回应等等。只有某些路径的移动会导致获胜，我们只想找到通往成功结局的路径之一。

作为一个经验法则，你想用BFS来寻找最短路径、测试图是否为二分图或查找所有连通分量。DFS用于决策树和搜索整个图空间。此外，BFS更适用于稀疏图，而DFS更适用于密集图。

在图嵌入中，不同技术尝试在BFS和DFS之间找到平衡，以探索邻域或发现网络：BFS算法强调同质性，而DFS强调结构等价性作为嵌入中捕捉的相似性类型（但这是另一个教程的内容）。

Python实现

我将展示如何使用Networkx实现我们上面绘制的图的算法。让我们设计并绘制一个图G：

#code to implement with networkx
import networkx as nx

graph = {
'1' : ['2','3'],
'2' : [ '4', '3'],
'3' : [ '7', '8'],
'4' : ['5', '3'],
'5' : ['6'],
'6' : [],
'7' : [ '8'],
'8' : []
}
G = nx.Graph(graph)
nx.draw(G , with_labels= True)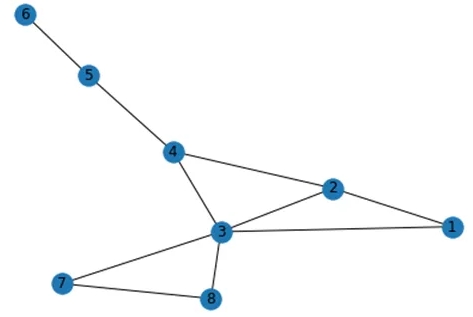

实现BFS非常简单：

source = "1"
path = nx.bfs_edges(G, source)
visited = [source] + [v for u, v in path]
visited

[‘1′,’2′,’3′,’4’,’7′,’8′,’5’,’6’]

同样适用于DFS：

source = "1"
path = nx.dfs_edges(G, source)
visited = [source] + [v for u, v in path]
visited

[‘1′,’2′,’4′,’5′,’6’,’3′,’7’,’8’]

请注意，DFS比BFS更快（每次执行的时间可能会有所不同）：

import time
start_time = time.time()
path = nx.bfs_edges(G, source)
print("--- Time execution BFS: %s seconds ---" % (time.time() - start_time))
start_time = time.time()
path = nx.dfs_edges(G, source)
print("--- Time execution DFS: %s seconds ---" % (time.time() - start_time))

— Time execution BFs:8.630752563476562e-05 seconds —
— Time execution DFs:9.918212890625e-05 seconds —

iGraph速度较慢，因此如果需要处理更大的图，请使用 NetworkX：

— Time execution BFs:0.0001499652862548828 seconds —
— Time execution DFs:0.8001430511474609375 seconds —

总之

• DFS和BFS是由迷失在迷宫中的数学家们发明的（令人难以置信的是有这么多数学家在迷宫中迷失方向，但我们是唯一能发明算法并走出迷宫的人）。
• BFS首先探索源节点的邻居，而DFS则试图远离源节点，深入探索网络。
• 它们都可以在线性时间内实现：对于图 G(V, E)，时间复杂度为O(V+E)。
• 当目标顶点（或解决方案）靠近源节点时，BFS更合适；相反，如果解决方案远离源节点，DFS更合适。
• DFS比BFS更快，而且DFS的内存消耗也比BFS更少。
• 你可以在这里找到上一篇文章。本文使用的所有代码可以在这里找到。所有教程链接和代码也将收集在这里。

结论

这些算法构成了许多应用和复杂的机器学习算法的基础。未来我们将看到这些算法如何影响如node2vec或NN图等应用程序。

感谢阅读！你还可以订阅我们的YouTube频道，观看大量大数据行业相关公开课：https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ；在LinkedIn上关注我们，扩展你的人际网络！https://www.linkedin.com/company/dataapplab/

原文作者：Salvatore Raieli
翻译作者：文玲
美工编辑：过儿
校对审稿：Jason
原文链接：https://ai.gopubby.com/graph-ml-graph-traversal-algorithms-in-a-nutshell-a80288a4d604