MMM：用于营销组合建模和广告支出回报率的贝叶斯框架

可扩展的互联网企业依赖于营销来推动增长。在一定规模上，很少有公司能够承受低效地获取客户。两个热门话题是企业投入大量资金将人工智能能力引入营销的领域：媒体组合建模（MMM）和客户生命周期价值（LTV）预测。两者都专注于增加组织在营销上部署的投资回报率。本文将介绍什么是MMM以及最佳应用它的方法。

MMM是一种技术,允许营销团队衡量其投资的影响及其对推动对话的贡献。由于可用于广告的平台数量激增，这项任务的复杂性在过去几年里迅速增加。这种现象将潜在客户分散到不同的媒体渠道，我们可以将这些渠道分为线下或线上渠道。传统的线下渠道没有数字支持，范围从报纸、广播、电视广告和优惠券到贸易展的展位。在线渠道呈爆炸式增长，公司会同时使用其中许多渠道，例如电子邮件、社交媒体、自然搜索、付费搜索、联盟营销和影响者营销。

值得注意的是，良好的MMM需要同样准确的数据驱动归因模型，即哪些渠道有助于获得特定客户。另外，请注意，虽然归因是在用户级别进行的，但MMM通常应用于获取渠道级别。数据驱动归因不在本文的讨论范围内。

在本文中，我们的重点有两个方面。首先，我们开发了一个贝叶斯模型，以提高每个媒体渠道表现的透明度。其次，我们优化预算分配，以最大化我们的关注变量，这里是收入。除了详细介绍贝叶斯方法在MMM中的应用外，我们还提供了使用公共数据集的实现和应用演练。我们测试了模型的准确性，并计算了每个渠道的广告支出回报率（ROAS）。最后，我们优化了一个假设的预算在三个渠道之间的分配，以最大化收入。如果你想了解更多关于数据的相关内容，可以阅读以下这些文章：
所有数据科学家都应该知道的三个常见假设检验
如何开始自己的第一个数据科学项目？
导航数据驱动时代：为什么你需要掌握数据科学基础
数据科学家常见的13个统计错误，你有过吗？

代码可在GitHub上获取：https://github.com/zaai-ai/lab

媒体组合模型：它是什么？

媒体组合建模通过衡量广告渠道的有效性并提供媒体支出对销售影响的透明度，为全球组织提供支持。这些模型在优化目标变量（如销售额、广告支出回报率、收入、转化率、客户终身价值等）方面，支持预算在各渠道间的分配决策过程，起到了重要作用。

过去几年，人们进行了许多研究，并提出了几种模型来尝试模拟支出对相关变量的影响。这些模型基于按地理区域汇总的每周或每月数据。我们感兴趣的是模拟因变量（一个或多个上述感兴趣的变量）与自变量之间的关系。一些自变量是显而易见的，例如跨渠道的广告支出。不过，我们可以扩展我们的方法，以包括价格、产品分销、通货膨胀、天气、季节性和市场竞争等更多相关影响。

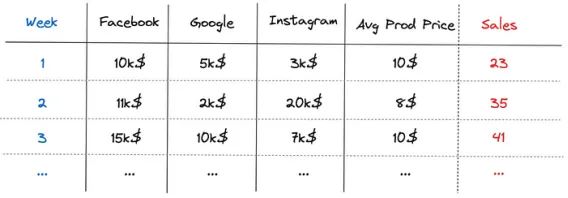
传统方法依赖回归方法从相关性中推断因果关系。然而，销售对媒体支出的响应不是线性的——存在饱和现象，这意味着在高水平支出时会有收益递减。此外，广告具有滞后或延续效应，这意味着前几周的支出可能会影响接下来几周的销售额。

媒体组合建模的贝叶斯方法

贝叶斯方法可以考虑饱和/形状和滞后/延续效应。

在深入研究模型细节之前，让我们先定义一个假设的数据集，以便更好地理解模型所采用的变量。假设我们有国家/地区级别的每周数据，其中每行代表一周( t)，每列代表媒体渠道 (m)或控制变量( c)，例如季节性或产品价格。渠道m在第t周的媒体支出定义为Xt,m，同一周的控制变量定义为Zt,c。

滞后或延续效应

延滞效应由一个名为adstock的函数建模。该函数创建特定渠道支出的累积效应。它通过当前周和前L-1周的媒体支出的加权平均值来转换其时间序列。L是特定媒体渠道的延滞效应的最大持续时间，它在估计加权平均方程中的权重Wm中起着重要作用。

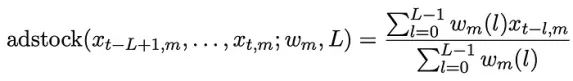
不同媒体渠道的L可以设置不同。这是一个由专家定义的超参数。如果某个特定渠道没有先验信息，作者建议将L设置为较大的数字，例如13，以捕获可能严重滞后的效果。

定义权重的方程可以有两种不同的形式：

1. 即时/几何广告库存，当广告效果的峰值发生在广告曝光同时，即在我们增加某个媒体渠道的支出的同一周，销售出现峰值。在方程2中，αm是广告效果的保留率。

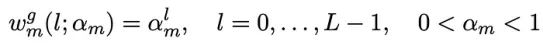
1. 延迟广告库存，广告效果峰值需要较长时间才能达到，并且不会立即对销售产生影响。在公式3中，θm表示峰值效果的延迟。

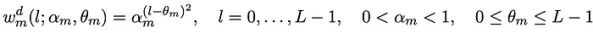
让我们使用我们的假设数据集，并计算Facebook渠道的即时广告库存和延迟广告库存。首先，我们在数据集中添加了5周的数据。我们假设广告效果的保留率（αm）为80%，峰值延迟（θm）为5周。之后，我们计算即时效应的权重和延迟效应的权重，以得到第8周的最终即时广告库存和延迟广告库存值。

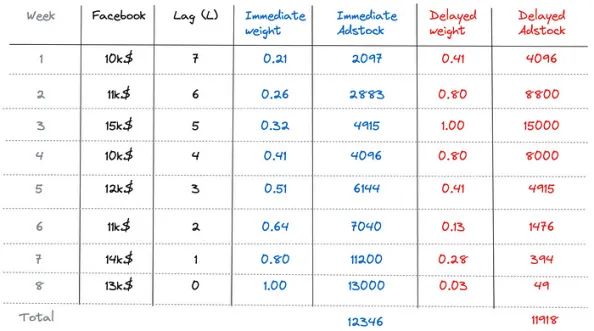
图3显示了第8周每周的支出对销售量的贡献。

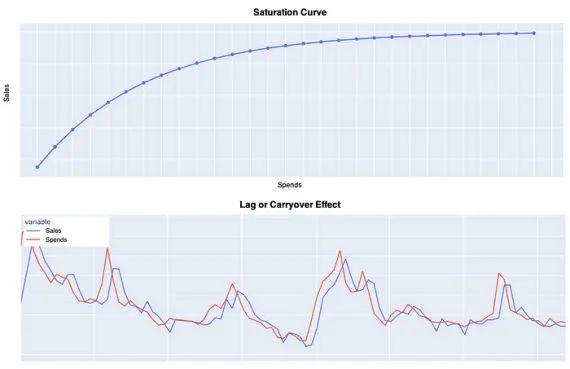
饱和度或形状效果

饱和度或形状效应通过曲率函数（例如逻辑饱和函数）变换媒体支出来建模。其定义如下：

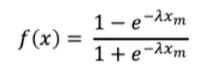
其中x代表媒体支出，λ控制饱和曲线的陡度，即决定媒体支出效应饱和的速度。然后，我们可以将较低的λ值解释为响应函数的更渐进的增加，这意味着媒体支出在很大的值范围内具有明显的影响。相反，较高的λ值将导致支出收益递减。图4非常清楚地显示了这些不同的行为。

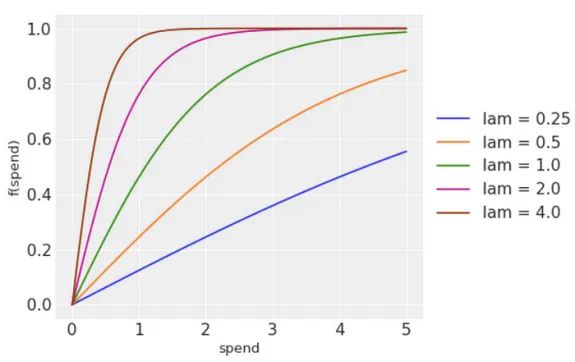
确定模型所需的参数是困难的，因为每个渠道的行为都非常特定。然而，在贝叶斯方法中，这些参数是使用先验分布来估计的。因此，模型会为给定的数据选择最可能的参数值。因此，我们必须设定一个分布而不是单个值。

结合延续效应和形状效应

如前两节所述，为了对延滞效应和塑造效应进行建模，我们需要将转换应用于每个渠道的媒体支出。这引出了一个问题：应该首先应用哪种转换。

• 如果媒体支出主要集中在特定时期，则形状效应将会延续。
• 如果媒体支出均匀分布在多个时间段，那么结转效应就会遵循形状效应。

由于组织通常倾向于集中其营销活动，因此最常见的方法是延续→塑造效果的组合。

尽管如此，第t周的因变量销售额y可以通过媒体支出和控制变量的线性组合来建模。我们还使用回归系数β来模拟不同媒体渠道的不同影响。

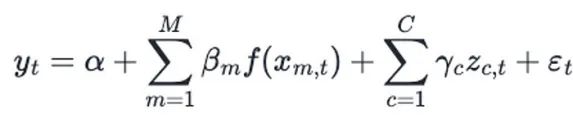
其中α是截距。函数f(xm,t)考虑了广告库存（残留）和饱和度效应，对介质对目标变量的贡献进行编码。γc是控制变量Zt,c的影响，et是白噪声。

贝叶斯模型

贝叶斯方法首先定义模型参数的先验分布，反映考虑数据之前的初始信念。随着新数据的引入，计算似然函数，该函数表示在给定参数的情况下观察数据的概率。在这种情况下，数据包括媒体渠道X和控制变量Z，它们解释因变量y。使用贝叶斯定理，通过结合先验分布和似然函数可获得后验分布。

作者依靠吉布斯抽样，因为它在选择每个媒体渠道（X）和控制变量（Z）的参数值时具有较高的抽样效率。

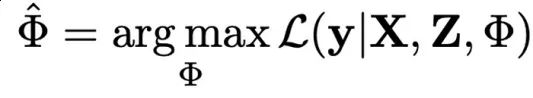
请记住，当数据携带强大信息且具有清晰模式时，模型较少依赖先验分布来估计参数。

尽管如此，作者还是留下了一些关于如何定义每个参数的先验分布的指导：

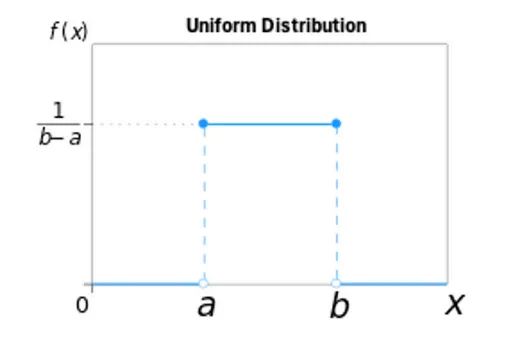
• 保留率（α）受限于[0,1[，应该在[0,1[上定义先验分布，如贝塔分布或均匀分布。

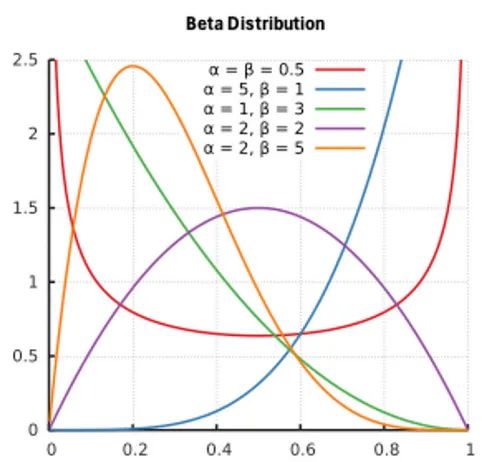
• 延迟参数（θ）通常限制在[0，L -1]上，并且应该具有先验，例如均匀或缩放的beta分布。

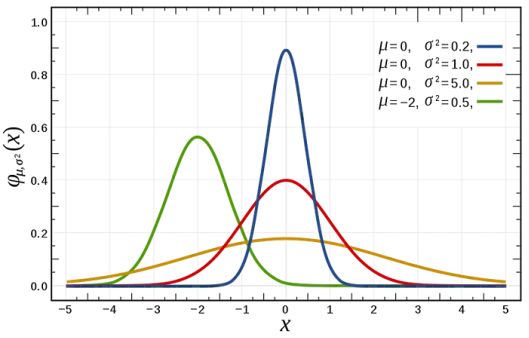
• Gamma(γ)和截距通常由正态分布建模。

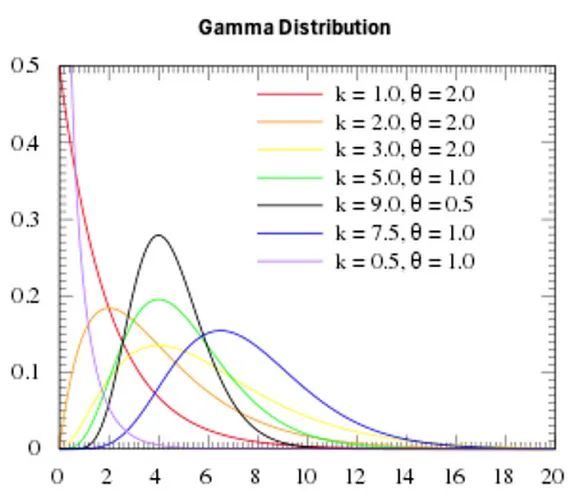
• Lambda(λ)通常由伽马分布建模。

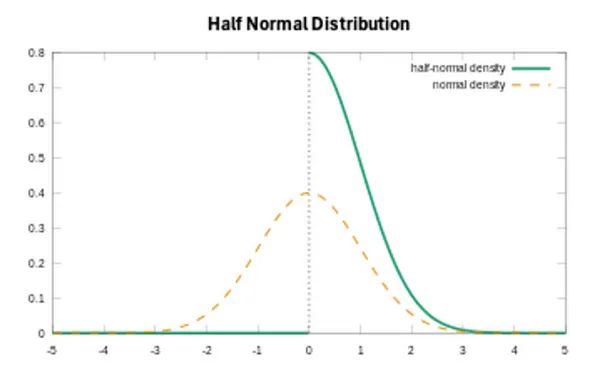
• 回归系数(β)通常由非负先验（例如正态分布）建模，因为媒体支出不会对y产生负面影响。

使用PyMC进行贝叶斯媒体组合建模

本节在一个来自Kaggle的公开数据集上实现贝叶斯模型，该数据集遵循CC0公共领域许可协议。该数据集包含关于三个不同媒体渠道（电视、电台和报纸）的支出信息以及同一时期的销售数据。

数据集由以下内容组成：

• ID—标识一行；
• TVAdBudget($)—电视广告支出；
• RadioAdBudget($)—广播广告支出；
• NewspaperAdBudget($)—报纸广告支出；
• Sales($)—目标变量。

拟合的贝叶斯模型将帮助我们计算每个渠道的ROAS、留存率和饱和度。除此之外，它还将帮助我们优化未来几周的预算分配。

为了估计模型的可靠性，我们将评估它在基于各媒体渠道支出和控制变量的未见数据上建模因变量的效果。我们采用回归指标，如平均绝对误差（MAE）。在基准测试方面，我们使用一个简单模型，该模型始终预测训练数据的平均值。顺便说一下，当没有MMM（市场营销混合模型）时，公司通常依赖这种方法。

我们首先导入库：

%matplotlibinline
%load_extautoreload
%autoreload2
importarvizasaz
importdatetime
importpandasaspd
importseabornassns
importmatplotlib.pyplotasplt
importnumpyasnp
importutils
frompymc_marketing.mmm.delayed_saturated_mmmimportDelayedSaturatedMMM
fromsklearn.metricsimportmean_absolute_error

然后，我们加载数据集并执行一些基本的预处理任务。我们简化了列名并根据ID添加了新的日期列。它有助于使用季节性和趋势等控制变量丰富数据集。

#loaddataandrenamecolumns
df=pd.read_csv('data/data.csv')
df=df.rename(columns={'Unnamed:0':'id','TVAdBudget($)':'tv','RadioAdBudget($)':'radio','NewspaperAdBudget($)':'newspaper','Sales($)':'sales'})

#createdatetimecolumn
df['ds']=df['id'].apply(lambdax:pd.to_datetime("2024-02-26")-datetime.timedelta(weeks=len(df)-x))

之后，我们进行一些探索性数据分析来了解数据内的相关性：

1.我们评估因变量与各个媒体渠道之间的相关性。

• TV是与销售额最相关的特征，而Newspaper相关性最差。

corr_matrix=df[['sales','tv','radio','newspaper']].corr()
sns.heatmap(corr_matrix,annot=True,cmap='Blues')
plt.show()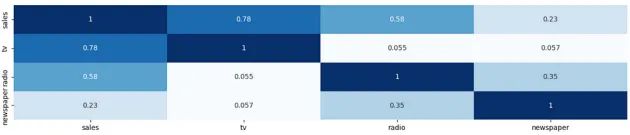

2. 我们绘制了销售额与各个媒体渠道的关系图，以评估支出峰值和销售额峰值之间是否存在滞后效应：

• 销售额没有明显的趋势或季节性变化。
• 电视广告的效果似乎对销售有直接的影响。
• 电台广告的效果也似乎对销售有直接的影响。例如，在2022年的第1、2和3周，电视广告投放较少，我们看到销售额出现了两次峰值，这与电台广告的峰值相吻合。
• 报纸广告的效果似乎有1-2周的滞后，但由于电视和电台广告同时投放，因此很难确定。

#onlysales
utils.line_plot(df.copy(),['sales'],'SalesoverTime')

#salesvstvspends
utils.line_plot(df.copy(),['sales','tv'],'SalesvsTVoverTime')

#salesvdradiospends
utils.line_plot(df.copy(),['sales','radio'],'SalesvsRadiooverTime')

#salesvsnewspaperspends
utils.line_plot(df.copy(),['sales','newspaper'],'SalesvsNewspaperoverTime')

完成探索性数据分析(EDA)后，我们可以开始准备建模部分，具体步骤如下：

1.将数据分为训练集和测试集：

train_df = df.sort_values(by='ds').iloc[:-5,:]
test_df = df.sort_values(by='ds').iloc[-5:,:]

2.利用之前生成的周数据提取趋势和季节性等控制变量。

我们利用Meta中的时间序列模型Prophet将时间序列分解为趋势和季节性，并将其作为控制变量。

seasonality, trend = utils.extract_trend_seasonality(train_df, 'sales', 5)
train_df.loc[:, 'seasonality'] = seasonality[:-5]
test_df.loc[:,'seasonality'] = seasonality[-5:]
train_df.loc[:,'trend'] = trend[:-5]
test_df.loc[:,'trend'] = trend[-5:]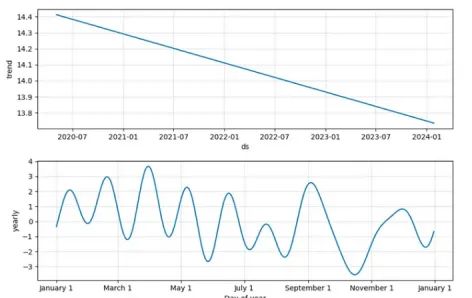

3.为模型设置不同的超参数。

这些参数可以通过传统的ML超参数搜索来定义。我们通过改变dist、mu和sigma值来优化一些回归指标。请记住，较高的标准偏差值（sigma）能让模型在搜索最优参数时获得更大的自由度。

my_model_config = {'intercept': {'dist': 'Normal', 'kwargs': {'mu': 0, 'sigma': 2}},
'beta_channel': {'dist': 'HalfNormal', 'kwargs': {'sigma': 2}},
'alpha': {'dist': 'Beta', 'kwargs': {'alpha': 1, 'beta': 3}},
'lam': {'dist': 'Gamma', 'kwargs': {'alpha': 3, 'beta': 1}},
'likelihood': {'dist': 'Normal',
'kwargs': {'sigma': {'dist': 'HalfNormal', 'kwargs': {'sigma': 2}}}},
'gamma_control': {'dist': 'Normal', 'kwargs': {'mu': 0, 'sigma': 2}},
'gamma_fourier': {'dist': 'Laplace', 'kwargs': {'mu': 0, 'b': 1}}}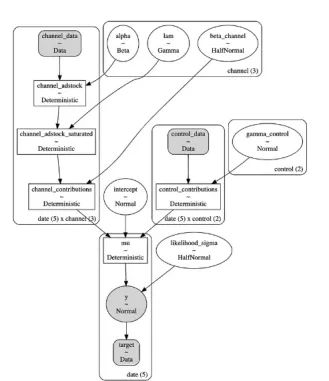

在图13中，我们展示了我们实施的模型的Kruschke图。它简明扼要地概括了我们前面所做的定义。在阅读这样的图表时，有几个方面需要考虑。请注意，我们可以在每个节点中找到变量及其各自的分布。例如，包含α的圆圈表示贝塔分布，如前所述。阴影节点代表观测变量。圆角方框表示重复。例如，由于我们有三个采集通道，我们为每个通道设置了一组不同的α、β和λ参数。箭头表示依赖关系。在我们的模型中，有两个箭头指向似然函数：一个表示对mu参数的依赖，另一个表示对sigma参数的依赖。mu参数本身还有另外三个依赖关系。回想一下，我们选择通过整合带入效应、形状效应和控制变量来建立销售模型。

现在我们已经定义了训练集和测试集以及模型配置，我们可以启动贝叶斯模型并将其与训练数据进行拟合。

媒体渠道[“电视”、“广播”、“报纸”］

控制变量[“季节性”、“趋势”］

根据EDA，最大广告滞后（延迟参数）似乎不超过2

mmm = DelayedSaturatedMMM(
model_config=my_model_config,
sampler_config={"progressbar": True},
date_column="ds",
channel_columns=["tv", "radio", "newspaper"],
control_columns=["seasonality", "trend"],
adstock_max_lag=2,
)

mmm.fit(X=train_df[['ds', 'tv', 'radio', "newspaper", "seasonality", "trend"]], y=train_df['sales'], target_accept=0.95, chains=4, random_seed=42)

拟合模型后，我们可以通过比较采样预测值（蓝色）和真实值（黑色）来检查模型与训练数据的拟合程度。在我们的例子中，它们非常吻合。

mmm.sample_posterior_predictive(train_df[['ds', 'tv', 'radio', "newspaper", "seasonality", "trend"]], extend_idata=True, combined=True)
mmm.plot_posterior_predictive(original_scale=True);

现在，我们可以开始用几种方法来解释模型：

1.检查参数估计：

广播的投资回报率似乎最高，因为其系数（β）最高（1.185），其次是电视和报纸。

电视的保留率α为3.2%，广播为2.3%，报纸为23.9%。

az.summary(data=mmm.fit_result,
var_names=[
"intercept",
"likelihood_sigma",
"beta_channel",
"alpha",
"lam",
"gamma_control",
],
)

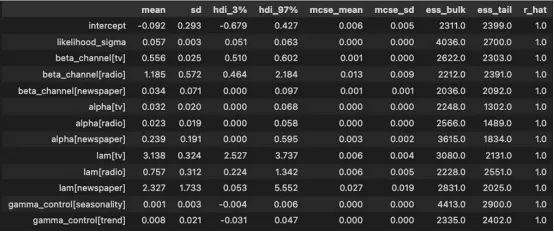
电视的饱和率λ较高（3.138），占总支出的73%。在图12中，我们可以更容易地比较3个频道的饱和率。

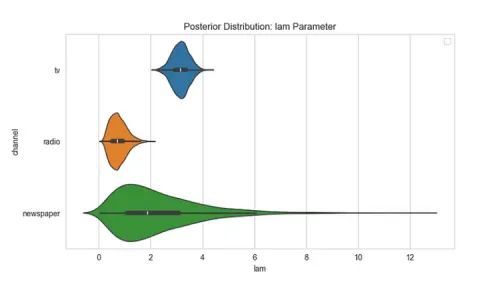
2.检查各渠道的贡献和ROAS（投资回报率）：

ROAS是通过将其中一个媒体渠道的支出设为零来计算的，以评估预测销售与当前销售的变化情况。例如，如果我们将报纸的媒体支出设为零，我们预计销售不会出现大幅下降。因此，其ROAS将较低。尽管电视的贡献最高，因为其支出较高，但我们可以看到模型预测广播的ROAS较高。

# channel contribution
fig = mmm.plot_channel_contribution_share_hdi(figsize=(7, 5))

# ROAS calculation
utils.plot_ROAS(mmm, train_df, ["tv", "radio", "newspaper"])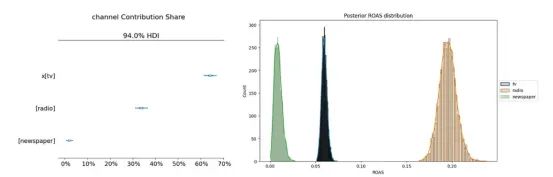

3.最后，我们还可以通过考虑带入效应和饱和效应，评估如果我们将每个渠道的广告支出增加50%会出现什么情况。

X轴是输入渠道数据的百分比水平：

• 当=1时，我们得到的是模型输入支出数据。
• 当=1.5时，我们得到的是如果我们增加50%的支出，会有多少贡献。

报纸似乎已经达到饱和点，因为增加50%的支出也不会带来更多的贡献。

从两条线的斜率来看，广播的饱和度似乎远低于电视。

plt.rcParams["figure.figsize"] = (20,5)
mmm.plot_channel_contributions_grid(start=0, stop=1.5, num=12);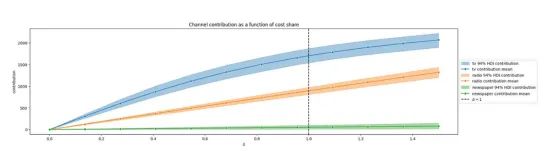

为了了解我们的结论是否有效，我们可以使用测试集来评估我们的模型根据媒体渠道和控制变量预测未来销售额的能力。为此，我们使用MAE并将其与原始模型进行比较。

我们的MAE为2.01，目标平均值为13.8。

我们的误差比基准低58%。

y_out_of_sample = mmm.sample_posterior_predictive(X_pred=test_df[['ds', 'tv', 'radio', "newspaper", "seasonality", "trend"]], extend_idata=False)
y_pred = [np.median(x) for x in y_out_of_sample['y']]

print(f"MAE: {mean_absolute_error(test_df['sales'], y_pred)} for an average target of {test_df['sales'].mean()}")
print(f"MASE: {mean_absolute_error(test_df['sales'], y_pred)/mean_absolute_error(test_df['sales'], [train_df['sales'].mean()]*5)}")

MAE:2.008733107943637，平均目标值为13.8 MASE:0.41701581608539257

回归结果表明，该模型是可靠的，能够很好地根据媒体渠道和控制变量对销售额进行建模。

预算分配

由于我们假设支出对销售额的影响不是线性的，因此会在某一点达到饱和。因此，我们需要确定哪种饱和函数更适合我们的数据。我们有两个函数选择来模拟饱和度：

α（alpha）是饱和点，这意味着支出的增加不会增加销售额；λ（lambda）影响曲线的斜率，数值越大，曲线越陡峭。

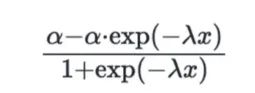
Michaelis-Menten函数，其中α (alpha)是通道的最大贡献值，λ (lambda)是曲线调整方向的时刻，即斜率。

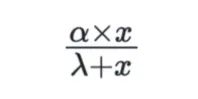
为了确定哪条曲线更适合我们的数据，我们将使用拟合的MMM计算每个函数的参数。然后，我们绘制这两个函数的曲线图，直观地检查哪一个拟合效果更好。

对于我们的具体情况，sigmoid函数的拟合效果更好。

# plot and extracting alpha and lambda
sigmoid_response_curve_fig = mmm.plot_direct_contribution_curves(show_fit=True)
sigmoid_params = mmm.compute_channel_curve_optimization_parameters_original_scale(method='sigmoid')

mm_response_curve_fig = mmm.plot_direct_contribution_curves(show_fit = True, method='michaelis-menten')
mm_params = mmm.compute_channel_curve_optimization_parameters_original_scale(method='michaelis-menten')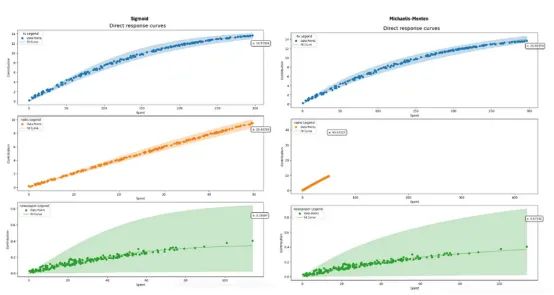

现在我们有了每种媒体渠道的西格米参数（α和λ），就知道了每种渠道的饱和点。因此，额外的支出不会增加收益，而在另一个渠道投入的资金却能达到预期效果。

我们可以使用一种算法，根据渠道饱和度、可用预算总额和每个渠道的预算限制来优化预算分配。PyMC实现了顺序最小二乘法二次编程（SLSQP）。在考虑到所有这三个变量的情况下，它能使所有信道的总贡献最大化：

• 总预算限制
• 每个渠道的最低和最高支出限额
• 饱和曲线

result_sigmoid = mmm.optimize_channel_budget_for_maximum_contribution(
method = 'sigmoid', #define saturation function
total_budget = 500, # total budget
parameters = sigmoid_params, # sigmoid parameters extracted previously
budget_bounds = {'tv': [75, 296], 'radio': [10, 300], 'newspaper': [1, 25]} # budget constraints by channel
)

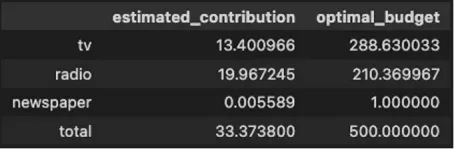
表4显示了我们的预算分配结果，其中广播是估计贡献最大的渠道，电视是建议我们花费预算最多的渠道。

市场不确定性下的预算分配

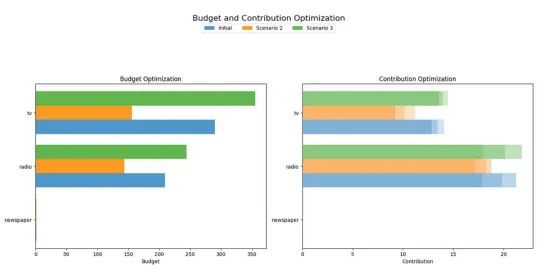
在当前的经济形势下，我们面临着很多不确定性。因此，我们必须设计一种预算分配策略，以适应各种情况。

让我们考虑三种不同的情况：

• 初始情景：经济保持稳定，预算分配与上一节计算的相同。
• 情景2：经济进入衰退期，预算削减40%
• 情景3：经济变得更加有利并开始增长，我们的预算增加20%。

我们将使用相同的拟合MMM模型和该模型的相同sigmoid参数来优化这些不同情景下的预算分配。我们将使用与之前相同的代码，但这次我们将循环使用不同的情景来减少或增加可用预算。

scenarios_result = []
total_budget = 500
channels = ['tv', 'radio', 'newspaper']

for scenario in np.array([0.6, 1.2]):
scenarios_result.append(
mmm.optimize_channel_budget_for_maximum_contribution(
method="sigmoid", # define saturation function
total_budget=total_budget * scenario,
parameters=sigmoid_params,
budget_bounds={
channel: [1, total_budget * scenario] for channel in channels
},
).to_dict()
)
_ = mmm.plot_budget_scenearios(
base_data=result_sigmoid, method="sigmoid", scenarios_data=scenarios_result
)

如图19所示，与初始情景相比，在衰退情景下，分配给电视的预算降幅明显大于广播。这在意料之中，因为正如我们之前看到的，广播的ROAS较高。另一方面，在增长情景下，分配给电视和广播的预算增幅相似。

结论

媒体组合建模的人工智能可以帮助我们获得积极的投资回报，获得有价值的忠实客户，也可以帮助我们在错误的媒体渠道和错误的客户之间耗费我们的财务资源。

在本文中，我们为营销组合建模开发了一个贝叶斯框架，它可以提供透明度并评估各公司媒体渠道获取新客户的进一步潜力。在我们的方法中，营销团队的领域知识可以通过设置先验分布的方式融入其中。这有助于提高模型理解媒体渠道与相关因变量（如销售额）之间关系的能力。最后，可以根据公司在获取新客户方面的投资能力来优化预算分配策略。在当今的宏观经济形势下，公司可能会转向盈利，从而减少用于投资增长的可用预算。我们展示了如何根据数据做出决策，在影响最小的情况下削减预算。反之，如果情况较为乐观，公司希望部署更多资源以加快增长，我们也会说明应在哪些方面进行投资。

我们目前正在各组织开发和部署新的人工智能应用。例如，我们正在利用生成式人工智能提升客户体验，利用时间序列预测改进规划流程。在这个案例中，我们展示了人工智能如何提高营销预算的效率。根据我们的经验，在采用人工智能方面，先进和成熟的组织需要一套专注于其核心活动的专门人工智能模型。

参考文献

1. Yuxue Jin, Yueqing Wang, Yunting Sun, David Chan, Jim Koehler. (2017). Bayesian Methods for Media Mix Modeling with Carryover and Shape Effects.
2. Dominique M. Hanssens , Leonard J. Parsons , Randall L. Schultz. (2003). Market response models: econometric and time series analysis. Springer Science & Business Media.
3. Hill, A. V. (1910). The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. Journal of Physiology, 40 (suppl), iv–vii. doi:10.1113/jphysiol.1910. sp001386.
4. Gelfand, A. E. & Smith, A. F. (1990). Sampling-based approaches to calculating marginal densities. Journal of the American statistical association, 85 (410), 398–409

感谢阅读！你还可以订阅我们的YouTube频道，观看大量大数据行业相关公开课：https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ；在LinkedIn上关注我们，扩展你的人际网络！https://www.linkedin.com/company/dataapplab/。

原文作者：LuísRoque
翻译作者：诗彤&Qing
美工编辑：过儿
校对审稿：Jason
原文链接：https://towardsdatascience.com/mmm-bayesian-framework-for-marketing-mix-modeling-and-roas-ccade4005bd5