什么使得一个预测模型可被解释？

机器学习（Machine Learning)中的可解释性(Interpretability)的确是一个非常有意思的问题。在Quora论坛中，有大量优秀的关于这个问题的涵盖模型复杂度，可理解性和可视化等方面的讨论。随着对这些问题的反复讨论，这里我有关于一些细微的差别之间的理解。

首先，根据定义，一个人是无法真正理解一个模型的。虽然这听上去很让人泄气，但是事实是：如果人脑的思考能力能够和一个优秀的机器学习模型并驾齐驱的话，那我们是完全可以理解这个模型的。但是根据定义，一个比人类更善于预测的模型则并不能真正的被人类理解。

在这里，想问大家一个问题：你有没有和一个数学家讨论过数学或与一个非常聪明的人对话过？（这好像总发生在我身上）一些人或许能比别人更好的解释某些问题，但是最终你却并不能明白他们所领悟的东西，或者像他们那样理解问题。就算我们认为自己真正的理解了这个问题，那所做出的解释也往往是一个“并不很正确”的简述。这套理论同样适用于对于模型的理解。但这是决定论的说法。相对而言，我们或多或少都能够理解这个模型是如何运作的。那就引出了我在这里想要讨论的细微差别：你到底是想要理解一个模型的具体原理，还是理解一个模型所做出的预测？这两者之间毫无疑问存在着着显著的区别。去理解的具体原理可以让你获得对建模过程更深入的理解。但是这有别于对一个具体预测做出解释，特别当你想让其它从业者们产生一个共同的预测的时候。

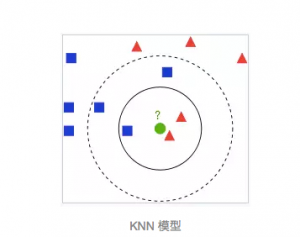
我常常与别人交流我的模型以及我对模型的理解，在与许多领域的业者的合作经历中，我选择过许多非常糟糕的模型，比如KNN模型。原因就是它不能“学习”，因为它并不能明确的告诉你一个维度或者一种特性比另一种更加重要。然而这却是机器学习最重要的核心基础：分析区别出什么是最重要的，什么是不重要的。KNN 不会“学习”，但是我们能非常容易理解它的预测原理，比如：你一定喜欢“特工佳丽”（Mrs Congeniality)这部电影，因为这些这些人喜欢的电影你也喜欢！因为他们喜欢，所以你就是会喜欢，你不能否认这个事实！其实从一个角度来说，这个方法其实非常有效，特别是与我们的主观想法结合起来。这就是我们所学到的：当我们遇到一个与曾经非常相似或与之产生共鸣的环境，我们就能知道下一刻会发生什么，就像我知道当我去触碰火焰时我会受伤。

nolvadex-tamoxifen.net，逻辑回归给得出一个0.9237的概率，事实上这是一个对于一组大量的，关于你对不同电影喜欢程度的指标量的线性组合的分对数变换。注意，在这个地方你完全可以用高中代数去充分“理解”这个模型，但这毫无意义，而且它忽略了我的上一个问题：为什么在那个方程中我对“异形”的评分要乘以-0.348？

当KNN模型的预测如此的容易交流的同时，模型本身的缺陷制约了它对问题本质探究的能力。其实，这里有非常多的东西需要通过逻辑回归去学习和理解。如果你上一个例子中被某个人喜欢的电影的二元指标，其中的参数可能足够去推断这个人可能会喜欢“特工佳丽”。不过就这个例子来说，我愿意用更简单的理论来解释，就是朴素贝叶斯理论（Naive Bayers)。在逻辑模型中log-odd可以混淆判断，比如去考虑这里的共线性会让结果产生错误，事实上，像“终结者1”的电影可以对喜欢“终结者3”的概率结果有不好影响，就算已知条件“终结者2”在其中不是一个积极的影响。当这些细微的差别让逻辑回归产生比朴素贝叶斯更好的预测时，其中的参数总是呈现“反直觉状态”的。所以我通常只是计算条件概率之间的比值去理解它们，而不是依仗自己的直觉。

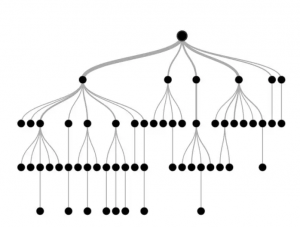
决策树状图的最终结果是能够被解释的，但一旦你有了足够的数据，树状图将会增大以至于不便于直观分析。甚至在一些小的树状图里，你可以写下预测标准，比如：因为你超过23岁，你会喜欢这部电影或这些电视剧。但你其实并没有解释什么，你不知道为什么树状图是以这种方式呈现。事实上，这些树状图会在算法下会因为非常小的样本改变有极端的变化，同时有非常多不同的树状图也能够呈现完全一样的集合划分。这说明了什么？首先，我们应该问自己我们到底想解释什么。我们的大脑常常以为“理解”了一个模型，但是往往大脑的理解是错误的。进一步解释，我们可以把一个模型当作一个黑匣子，其中通过不同的输入得到这个模型对于输入量微扰的敏感度。现在我让这个模型来预测我是否比真实的我大10岁。这其实与IID抽样理论不一致， 但我认为这至少是一个公平的测试。

有许多方法可以去用一个模型去理解一个领域甚至变量之间的关系，但是大多数其实就是利用数据分析历史上最基本的法则。其实在观测法领域（比如TMLE和其他robust estimators)工作有意思的是：我们其实不在意一个模型的解释能力。一个普通的解释通常都从模型预测中来，而不是它的具体构造。其实，鲁棒性（robustness)保证中的一致性起因于模型中的一种，简单来说也就是更少的解释性。