Sampling 101：详解统计学中的抽样技术

统计学是通过搜索、整理、分析、描述数据等手段，以达到推断所测对象的本质，是数据科学的重要组成部分。每当我们遇到统计研究时，都会听到很多不同的统计术语，其中最常听到的术语之一就是抽样。在本文中，我们会带你了解什么是抽样，然后再深入探讨不同抽样技术的细节。

简单地说，抽样是从总体中选择一组(样本)，我们再从中收集可用于研究的数据。抽样是研究的一个重要部分，因为研究成果在很大程度上取决于所用的抽样技术。因此，为了得到准确的结果，或想要很好地预估总体的结果，就需要选择合理的抽样技术。如果你想了解更多数据分析相关内容，可以阅读以下这些文章：
AB 测试应用：AB Testing在社交领域的实践及挑战
数据科学家八大最常见统计面试题
长文总结在机器学习中处理倾斜数据集

我们先从统计学的角度来了解，究竟什么是样本和总体。

总体（Population）是我们从中抽取统计样本进行研究的元素或个体资源的集合，最终我们要对这一整个总体作出结论。总体中包含的元素或个体的数量被称为群体大小（population size）。

注：在统计研究中，总体（Population）并不总是指的人。它可以是任何东西，比如印度的羊的数量；美国所有小学生的人数；互联网上所有博客网站的数量。

另一方面，样本又是总体的一个子集，它是你收集数据的特定组。样本中元素或个体的数量称为样本容量（sample size），选择样本的过程就称为抽样（sampling）。例如，印度拉贾斯坦邦州的绵羊样本；美国纽约的小学生样本；互联网上的数据科学博客相关的网站样本。

注：样本的大小总是小于总体的大小。

那么，我们为什么需要样本？🤔这是一个很好的问题，👏让我们首先来了解这一点。

为什么我们需要样本？

答案很简单，也很直接。几乎不可能从总体中的每一个个体(或元素)收集数据，因此，抽样有助于我们获得关于整个总体的信息。很明显，结果不可能完全准确，但会接近于整体。此外，重要的是，所选的样本应该要代表总体，不能带有任何偏见。

这是一个从人群中抽取样本的简单图例。

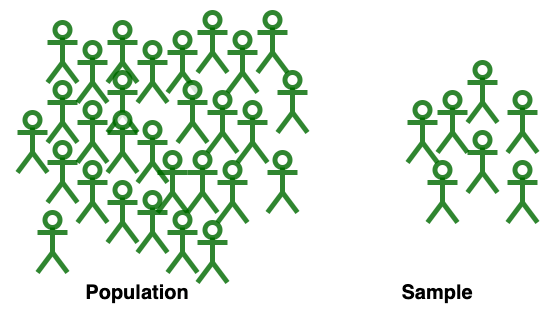
抽样技术其实有很多，但我们在这里只讨论一些统计中常见的抽样技术，也不会对这些技术进行太多的比较。

简单随机抽样（Simple Random Sampling—SRS）

假设总体是20个人，我们需要从中抽取7人作为样本。为了方便理解，我们给这些人进行编号。现在，我们在1到20之间随机选择7个数字，与这些数字相对的人将成为我们样本的一部分。如果所选数字对应的人已经在我们的样本中，我们就跳过那个数字并选择另一个数字。

假设我们选4，然后7，然后11，然后20，然后1，然后12，然后20。既然20已经被选过了，那我们再选一个数字，假设选19。为了便于理解，我们把选中的人划掉。

注意：

• 我们跳过重复的数字，因为现实中我们不会对同一个人进行两次调查或采访。
• 产生随机数有很多不同的方法，你可以通过编程的方式来实现，也可以将所有数字放在一个袋子中，每次选择一个。

这种类型的抽样被称为简单随机抽样（simple random sampling）。当总体是同类的时候，这种抽样方法是最合适的。可以注意到，样本中的每个成员都有相等的选择机会(概率)，在这种情况下，选择的概率是1/20。

分层抽样（Stratified Sampling）：

我们还是用和上面一样的例子。假设这次的样本容量是9。我们根据这些人所穿的衣服的颜色把他们分成不同的组。

根据颜色，我们将从这20个人划为4组。这些小群体中的每一个都被称为一个层（stratum），而每一个层都可以被一个特征定义，在这里就是衣服的颜色。因此，层是根据样本成员的先决条件创建的。一个层的成员是同类的，一个层的成员与另一个地层的成员是异类的。因此，当总体本身是异类的，但同类的层可以从中分离出来时，就可以使用这个抽样。

现在，从每一层中选择一个成员，也就是说，从每一层中抽取一个样本。当我们对一个有许多不同层的总体进行抽样时，通常要求样本中每个层的比例应与总体中的比例相同。

为了简单理解这个概念，这里举一个简单的例子：

• 黑色的比例=(黑色数量/总数量)*样本量= (9/20)*8 = 3.6
• 红色比例= (4/20)* 8 = 1.6
• 蓝色比例= (4/20)* 8 = 1.6
• 绿色比例= (3/20)* 8 = 1.2

如果我们选择近似的数字，可以选4个黑色，2个红色，2个蓝色和1个绿色来代表总体。

注：从单独的层中抽取样本时，可以采用随机抽样或其他任何抽样技术。

整群抽样（Cluster Sampling）：

人们经常会混淆整群抽样和分层抽样，但这两种抽样方法是不同的。主要的区别是，在整群抽样中，你用自然组将总体分类。例如，城市街区、学区、年龄、性别等等。

我们再次考虑以上的总体，假设第一排的人住在第36街，第二排的人住在第11街，每一排是一个集群。

现在，我们可以从这两个集群中选择一个集群(这可以通过简单的随机抽样完成)。假设我们选择第11街，那么我们将调查住在第11街的每一个人。

注意：我们可以选择随意数量的集群。

整群抽样可以通过两种方式进行：

单阶段整群抽样（Single-stage cluster sampling）：

即随机选择整群并调查整群中的每一个成员。

两阶段整群抽样（two-stage cluster sampling）：

即首先随机选择整群，然后从被选中的整群中随机选择成员。

系统抽样（Systematic Sampling）:

在这种抽样技术中，我们系统地选择成员。在这里是指，通过把所有成员排序为一个列，再以固定间隔选择成员。

让我们考虑一下20个人的样本总体。假设我们要选5个人，我们的系统是从第三个人开始，每四个人选一个。一直这样做，直到我们的样本选定5个人。(勾号代表已选人员。)

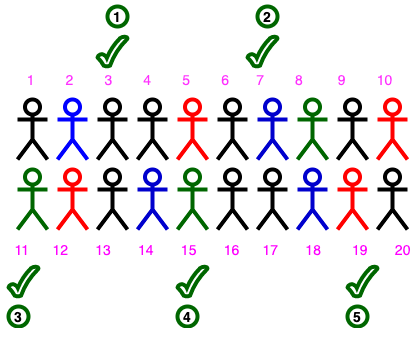
注意：

• 为了使每个成员都有平等的选择机会，建议采用随机抽样的方式选择第一个(起点)成员。
• 系统抽样可能导致偏差。

便利抽样（Convenience Sampling）：

它是最简单的抽样技术之一，但也是最危险的抽样技术之一，因为它是根据可用性来选择样本的。比如，调查你办公室里的每一个人，调查当地的每一只猫，这样的人和猫的样本都不能代表总体。

注：应使用随机化方法，让我们的样本能很好地代表总体，并能更接近关于总体的准确结果。

简单抽样技术、整群抽样技术、分层抽样技术和系统抽样技术都是概率抽样技术，都会涉及到随机化。然而，便利抽样是一种非概率(或非随机)抽样技术，因为它取决于研究者选择样本的能力，而非概率抽样技术可能会导致样本和结果的偏差。

还有很多其他抽样技术。例如，目的抽样（Purposive Sampling）、配额抽样（Quota Sampling）、滚雪球抽样（Referral/Snowball Sampling）等都是非概率抽样技术。多级抽样(Multistage sampling)是一种概率抽样技术。但是，讨论所有的抽样技术已经超出了本文涉及的范围。😐

希望本文能帮你理解这些抽样技术背后的基本概念。😀

参考文献：

这篇文章的灵感来自Steve Mays在YouTube上的一些精彩的视频：

https://www.youtube.com/channel/UC5IFOnQu-C3YmkLJltVAq2A

🙏还有，看看这个名为StatQuest(的神奇频道：

https://www.youtube.com/channel/UCtYLUTtgS3k1Fg4y5tAhLbw

希望本文能帮你理解这些抽样技术背后的基本概念。你还可以订阅我们的YouTube频道，观看大量数据科学相关公开课：https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ；在LinkedIn上关注我们，扩展你的人际网络！https://www.linkedin.com/company/dataapplab/

原文作者：Cameron Warren
翻译作者：过儿
美工编辑：过儿
校对审稿：Jiawei Tong
原文链接：https://towardsdatascience.com/sampling-techniques-in-statistics-9c77a39e0948