红酒数据集Case Study：一个分类问题

本文中的红酒数据集由 13 个不同的红酒参数组成，如酒精和灰分含量，包含了 178 个红酒样品的测量结果。这些红酒产于意大利的同一地区，但来自三个不同的栽培品种；因此，有三种不同的酒。

本文目标是找到一个设计模型，可以根据提供的13个测量参数，预测红酒品种，并找出他们之间的主要差异。这是一个分类问题，而本文会列举四种模型，并评估每个模型的准确性。此外，我还会使用主成分分析，识别并探索三种红酒之间的差异。如果你想了解更多数据分析相关内容，可以阅读以下这些文章：
用数据科学技术，分析用户产品倾向
一文上手用Pandas给数据加标签
你总说没有经历没人要？这24个全网公认最有价值的开源数据项目你做了么？
如何巧用数据可视化，讲好一个故事？

多项逻辑回归
（Multinomial Logistic Regression）

由于有三种红酒，我们必须使用多项逻辑回归，而不是用两项的逻辑回归。因此，我使用了 nnet 包中的multinom函数。

> dim(wine)
[1] 178 14
> attach(wine)
> test=sample(178,45)
> library(nnet)
> LogReg=multinom(class~.,data=wine[-test,])
> summary(LogReg)
> Pre=predict(LogReg,wine[test,])
> table(Pre,wine[test,]$class)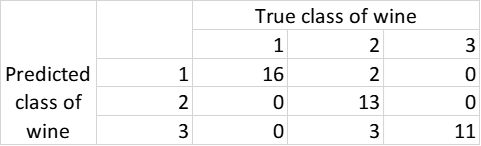

从表 1 中可以看出，45 个观测值中有 5 个错误的分类；所以，多项式逻辑回归模型的准确率为 89%。

我们可以多次执行以下命令，更加准确地评估多项逻辑回归模型的性能：

> Accuracy=rep(0,50)
> for (i in 1:50) {
+ test=sample(178,45)
+ LogReg=multinom(class~.,data=wine[-test,])
+ Pre=predict(LogReg,wine[test,])
+ Accuracy[i]=mean(Pre==wine[test,]$class)
+ }
> sum(Accuracy)/50
[1] 0.944

线性判别分析
(Linear Discriminant Analysis——LDA)

当我们有两个以上的类，并且观察的数量很少时，LDA 会非常有用。当预测变量在每个类别中的分布都为正态时，LDA 的准确率也更加稳定。

> library(MASS)
> lda.fit=lda(class~.,data=wine[-test,])
> lda.fit

最后一个命令将生成有关模型的更多详细信息，如表 2 所示。

> lda.pred=predict(lda.fit,wine[test,])
> table(lda.pred$class,wine[test,]$class)

接着，我们评估模型对于测试数据表现出的性能：

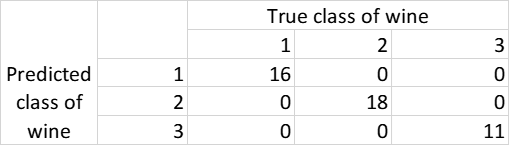
从表 3 中，我们可以看出，LDA 在预测测试数据类别方面的准确率为 100%。

我们还可以执行以下命令，可视化 LDA 对训练数据的分类，结果如图 1 所示：

> plot(lda.fit)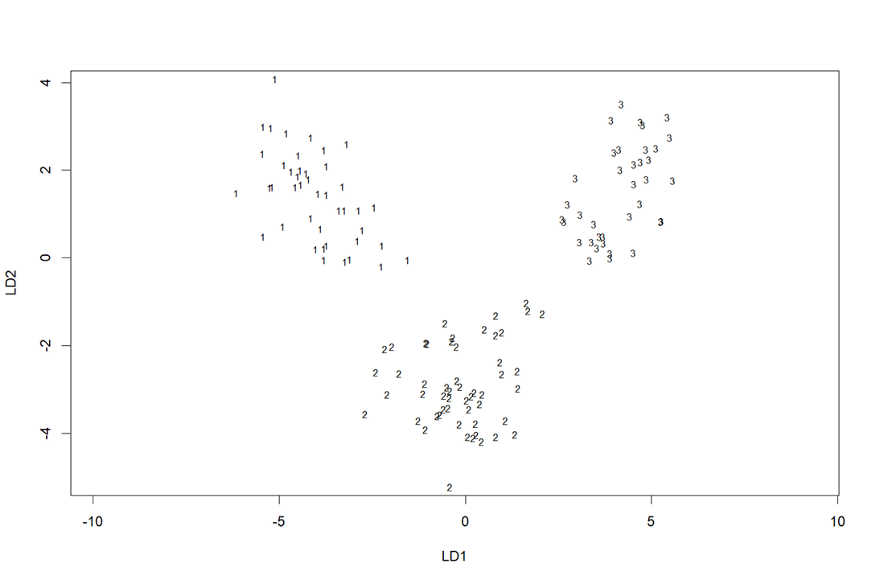

由于数据集中有三个类，因此，我们只需要两个线性判别式来对观察结果进行分类。 图 1 显示了 LD1 和 LD2 空间上的训练数据图，以及每个数据点的相应类。根据LDA模型系数，我们可以得出LD1和LD2值。

我们可以多次执行以下命令，更加准确地评估 LDA 模型性能：

> for (i in 1:50) {
+ test=sample(178,45)
+ lda.fit=lda(class~.,data=wine[-test,])
+ lda.pred=predict(lda.fit,wine[test,])
+ Accuracy[i]=mean(lda.pred$class==wine[test,]$class)
+ }
> sum(Accuracy)/50
[1] 0.9844444

二次判别分析
 (Quadratic Discriminant Analysis——QDA)

另一个分类器是 QDA 模型，其语法与 R 中的 LDA 相似。我们可以多次执行该操作，更加准确地评估 QDA 模型性能，如下所示：

> qda.fit=qda(class~.,data=wine[-test,])
> qda.pred=predict(qda.fit,wine[test,])
> table(qda.pred$class,wine[test,]$class)
> for (i in 1:50) {
+ test=sample(178,45)
+ qda.fit=qda(class~.,data=wine[-test,])
+ qda.pred=predict(qda.fit,wine[test,])
+ Accuracy[i]=mean(qda.pred$class==wine[test,]$class)
+ }
> sum(Accuracy)/50
[1] 0.9866667

K-最近邻 
(K-Nearest Neighbors —— KNN)

KNN 是一种非参数方法，根据其 K 最近邻的类对观察值进行分类。当决策边界为非线性时，该模型非常有用，但我们无法从中得知哪些预测变量更重要。

> library(class)
> knn.pred=knn(wine[-test,2:14],wine[test,2:14],wine[-test,]$class,k=1)
> table(knn.pred,wine[test,]$class)
> mean(knn.pred==wine[test,]$class)
[1] 0.7777778

我们可以多次执行以下命令，更加准确地评估 KNN 模型性能：

> for (i in 1:50){
+ test=sample(178,45)
+ knn.pred=knn(wine[-test,2:14],wine[test,2:14],wine[-test,]$class,k=1)
+ Accuracy[i]=mean(knn.pred==wine[test,]$class)
+ }
> sum(Accuracy)/50
[1] 0.7435556

我们可以对 k=2 到 5 重复相同操作，结果如表4中列所示。

从表 4 的中间一栏，我们可以看到 ，KNN 模型的效果不是很好。这是因为 KNN 模型使用欧几里得距离（Euclidean Distance）测量两点之间的距离，如果特征具有不同的尺度，就会影响模型效果。

由于这 13 个特征中具有不同的尺度，因此对数据进行标准化处理具有相同的值范围非常重要。我们可以在缩放数据后，重新运行 KNN 模型，如下所示：

> for (i in 1:50){
+ test=sample(178,45)
+ knn.pred=knn(scale(wine[-test,2:14]),scale(wine[test,2:14]),wine[-test,]$class,k=1)
+ Accuracy[i]=mean(knn.pred==wine[test,]$class)
+ }
> sum(Accuracy)/50
[1] 0.9382222

KNN 模型的结果如表 4 所示，我们可以看到，缩放数据大大提高了模型性能。

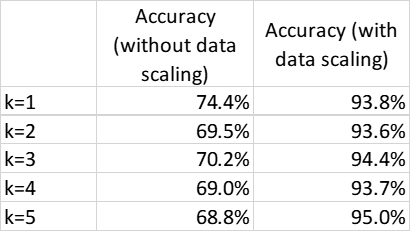
总结

表5总结了这几种分类模型下红酒数据集的准确率。LDA和QDA的准确率最高，其次是KNN（k=5）模型。

主成分分析 
(Principal Component Analysis——PCA)

上述模型可以根据 13 个预测变量预测红酒类别。然而，我们也很想知道这三个类别之间的主要区别，以及哪些预测变量最重要。我们可以通过探索性数据分析工具—主成分分析(PCA)执行以上操作。

> pr.out=prcomp(wine[,-1],scale=TRUE)
> pr.out$rotation
> biplot(pr.out,scale=0)
> plot(pr.out$x[,1:2],col=wine$class)

前两个主成分得分和相应的加载向量如图 2 所示。

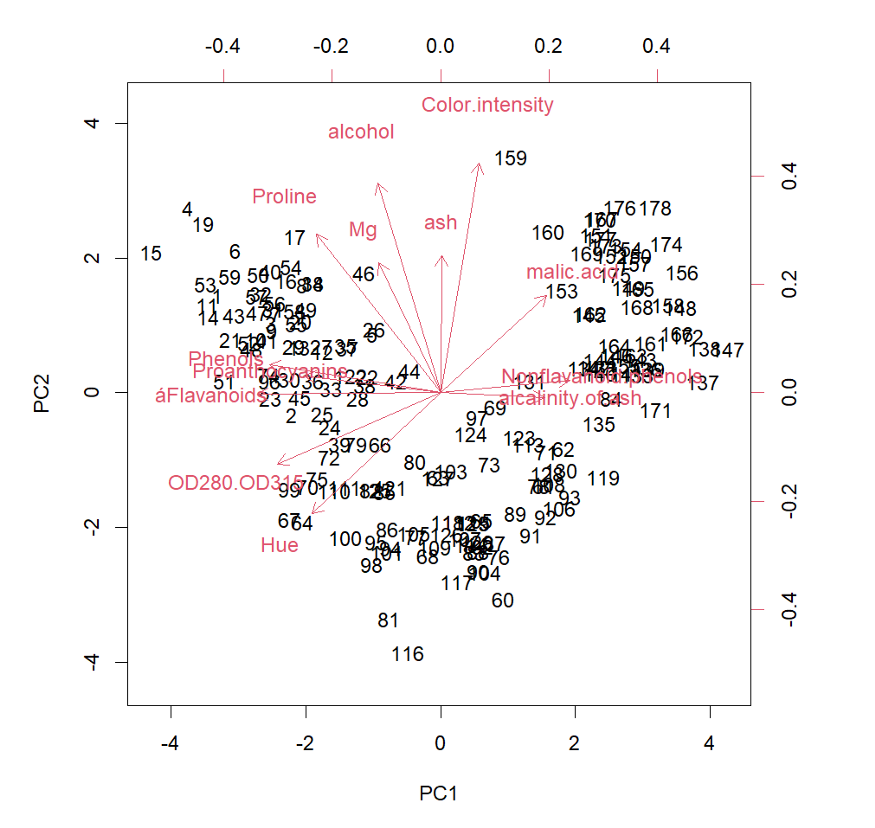
每个箭头表示在顶部和右侧轴上的前两个pc的加载矢量。图中的每个数字代表该特定数据点的 PC1 和 PC2 得分（图片由作者提供）

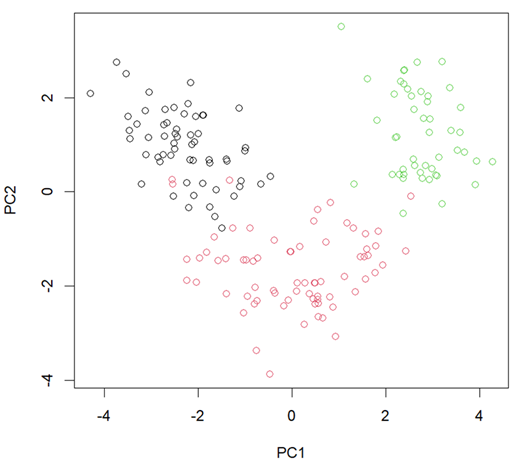
黑色代表第一类酒，红色代表第二类酒，绿色代表第三类酒 （图片由作者提供）。

图 2 和图 3 显示数据点被分为三个不同的组，对应三类红酒。第一类和第三类酒的PC2 得分相同，但PC1 得分差异较大。另一方面，第二类酒的PC1 得分介于第一类酒和第三类酒之间，其PC2 得分低于其他两类酒。我们可以通过查看 PC 加载向量（图 2 中的箭头），进一步查看每个类之间的差异。例如，“灰分碱度”的方向是 PC1 和第三类酒数据点的高值。 

因此，我们可以预测，第三类酒的“灰分碱度”值相对较高，其次是第二类和第一类酒。我们可以对其他 13 个预测变量执行类似操作。结果如表 6 和表 7 所示，显示三类红酒之间主要区别。结果与表 2 所示的 LDA 结果一致。

对于上述参数，第2类酒的值介于第一类和第三类之间。

结论

本文使用四种分类方法，评估每个模型在预测红酒类别方面的准确性。QDA 和 LDA 的准确度最高，其次是 KNN 和多项逻辑回归。在应用 KNN 模型进行准确分类之前，对数据进行标准化处理非常重要。主成分分析(PCA)用于确定三类红酒之间的主要差异。

你是否用过这几个模型？用在什么样的数据集中？欢迎你在文章下方留言！你还可以订阅我们的YouTube频道，观看大量数据科学相关公开课：https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ；在LinkedIn上关注我们，扩展你的人际网络！https://www.linkedin.com/company/dataapplab/

原文作者：Ali Faghihnejad
翻译作者：Lia
美工编辑：过儿
校对审稿：Jiawei Tong
原文链接：https://towardsdatascience.com/wine-data-set-a-classification-problem-983efb3676c9