一篇清单，带你了解决策树Decision Tree术语

如果你刚刚接触学习机器学习领域，你可能会感到非常困惑，尤其是袋装法（Bagging）、提升法(Boosting)、集成方法（ensemble methods）和随机森林（Random forest）这些决策树相关的术语和概念，也难免会抗拒学习这些深奥的知识。

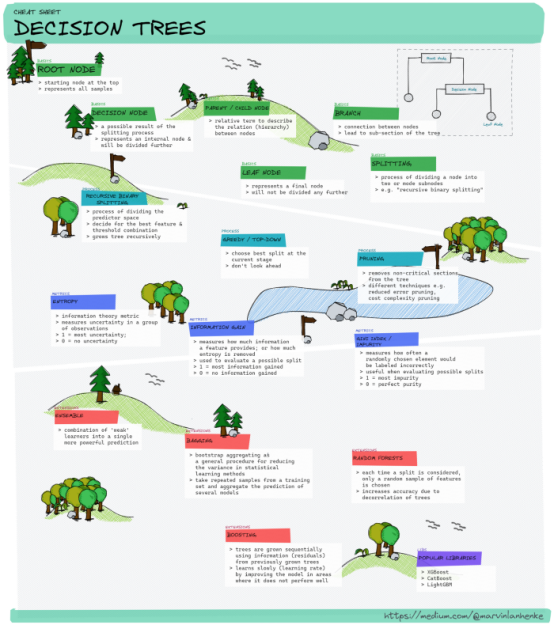
在下面的介绍中，我们来试着创建一个备忘单（Cheat-Sheet），帮助我们快速、全面解决策树领域内的概念。如果你想了解更多数据分析相关内容，可以阅读以下这些文章：
Merry Christmas～ 请收下刚从圣诞树上摘下来的6个新年新Flag!
如何画XGBoost里面的决策树？
Tableau数据可视化，学完就掌握商业分析必备技能了！
群体学习（Swarm Learning）的工作原理——结合区块链和机器学习的更优解决方案

免责声明：由于备忘单的性质，我们只能利用其对某些主题进行一般性的概述，因此无法详细介绍所有内容。

基础知识

在我们了解更加高级更花里胡哨的内容之前，我们先了解一些基础知识——了解决策树的主要组成部分，打好基础。

根节点（Root Node）

决策树也可以解释为一系列节点，即从单个节点开始的有向图。这个起始节点称为根节点，代表整个样本空间。

从根节点开始，我们可以根据不同特征和阈值划分或分裂样本空间，从而生成决策树。

分裂（Splitting）

分裂，即将一个节点划分为两个或多个子节点的过程。决策树的分裂方法很多，涉及不同的指标（例如信息增益（Information Gain）、基尼杂质（Gini Impurity））。

决策节点（Decision Node）

决策节点是根据拆分的结果定义。如果一个子节点分裂成更多的子节点，我们将这些节点称为决策节点或内部节点。

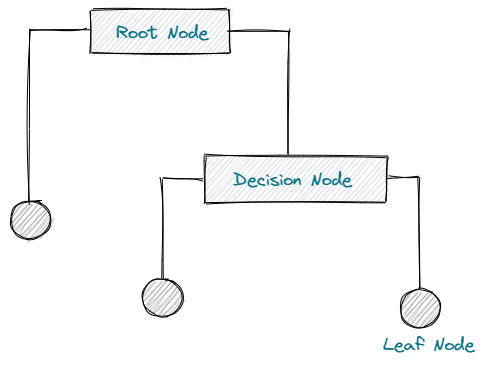
叶节点（Leaf Node）

如果某子节点不能进一步分裂，我们称该节点为叶节点。叶节点表示用于预测的响应值（例如最常见的类标签）。

分支（Branch）

分支描述节点之间的连接或决策树的子部分。

父/子节点（Parent/Child Node）

描述节点之间关系的相对术语。所有属于另一个节点的节点都是子节点。在这些子节点之前的任何节点称为父节点。 

建立决策树

现在，我们知道了决策树的基本组成部分，现在让我们来学习如何建立决策树。

递归二进制分裂（Recursive Binary Splitting）

建立决策树，会将输入空间划分为几个不同，且不重叠的子空间的过程。为了分裂输入空间，我们必须测试所有特征和阈值，从而找到最小化成本函数的最佳分裂方法。

一旦我们得到了最佳分裂方法，我们就可以继续递归增长树的数量。

该过程被称为递归，因为每个子空间可以无限次分裂，直到达到停止标准（例如最大深度）。

贪婪分裂（Greedy Splitting）

寻找最佳分裂，包括评估所有可能的特征和分裂点。由于我们只关心当前的发展阶段，没有考虑今后可能出现的情况，我们正在以贪婪的方式选择最好的分裂方式。

剪枝（Pruning）

删除非关键部分可以减少决策树的大小和复杂度。如此一来，泛化、过度拟合、以及预测准确性的效果都会更好。剪枝的方式也很多，主要有以下几种：

例如，减少错误剪枝，即用最常见的类标签替换节点。如果不影响准确性，则保留更改。

另一方面，代价复杂度剪枝（Cost-Complexity Pruning）则可能删除对精度影响最小，但完整保持其复杂度的完整子树。

指标（Metrics）

仅仅了解建立决策树的过程是远远不够的。为了评估所有可能的拆分方式，并能够合理地选择最佳的拆分方式，我们需要通过某种方法，评估分裂的质量或有用性。

评估指标如下。

熵（Entropy）

在信息论中，熵评估一组观测结果中的信息或不确定性的平均水平。其正式定义为：

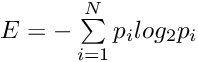
熵值为 1 表示不确定性最大，而熵值为 0 表示非常确定。

信息增益（Information Gain）

信息增益提供了一种评估方式，用于描述某特征提供了多少信息——或者换句话说，删除了多少熵。

我们可以通过从父类的熵中减去子类的加权熵，计算信息增益。因此，信息增益对于评估可能的拆分方式非常有用，帮助我们找到并选择最佳拆分方式。

信息增益为 1 是最佳值，而 0 表示非常确定性或没有完全删除熵。

基尼杂质（Gini Impurity）

用来评估随机选择的元素被错误标记的频率。该指标提供了一种测量节点纯度的方法，一方面，如果其值为 0，则表示纯度很高；另一方面，如果其值为 1，则描述杂质最多。

基尼杂质也可用于评估可能的分裂方法，其计算公式如下：

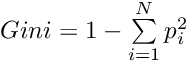
扩展方式（Extensions）

决策树解释起来会比较容易，因为它模仿了人类做出决策的过程，但有时可能不太准确或不稳定。

为了克服这些缺点，可以应用许多技术和扩展方式。

集成方法（Ensemble Method）

该方法是一种机器学习技术，将多个“弱学习模型”或构建块组合成更强大的预测结果。在本示例中，构建块可以是简单的回归或分类决策树。

装袋法（Bagging）

这个专有名词是自举汇聚法（bootstrap aggregating）的缩写。它是减少统计学习方法方差的一般程序，通过合并和平均观察数据集，用来减少方差。

在实际操作中，我们通过从单个训练集中随机抽取替换样本，并建立决策树来进行引导。重复该过程将产生多个可以聚合的决策树。

例如，在回归树中，我们通过取预测值的平均值聚合多棵树。将袋装法应用于分类树中，需要对预测的类标签进行多数投票，以便进行聚合。

随机森林（Random Forest）

通过对决策树的去相关，我们可以构建并改进袋装法的概念。在每次考虑分离时，我们只选择一个随机的特征样本m。这意味着，在分裂算法时，我们无法考虑大多数可用的特征。

虽然一开始感觉有些违反直觉，但它的主要思想仍然是有道理的。

例如，在构建袋装树时，算法可能只考虑一个特定的强特征。

因此，大多数树看起来会没什么区别。对大部分看起来相似的树进行平均处理，不会提高准确性，因为对高度相关的变量进行平均处理不会大幅降低方差。

提升方法（Boosting）

到目前为止，我们介绍的扩展都涉及构建多个独立的树。Boosting略微不同，它通过构建多个依赖于先前树的树。

在实际操作中，我们建立了几棵较小的树，其中每棵树都与前一棵决策树的残差相匹配。因此，我们需要慢慢改进模型中表现不佳的地方。

结论

在本文中，我们创建了一个备忘单（Cheat-Sheet），在术语的随机森林中找到自己的方法，该备忘单可以作为快速参考以及围绕决策树学习方法主题的总体概述。

由于我们只能简单概述，有些概念还可以进行更深层次的解析。但是，简单了解一些概念可以帮助你确定感兴趣的领域。你有没有用过决策树？还有哪些专有名词需要讨论？欢迎在文章下方留言！你还可以订阅我们的YouTube频道，观看大量数据科学相关公开课：https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ；在LinkedIn上关注我们，扩展你的人际网络！https://www.linkedin.com/company/dataapplab/

原文作者：Marvin Lanhenke
翻译作者：Lia
美工编辑：过儿
校对审稿：Jiawei Tong
原文链接：https://towardsdatascience.com/cheat-sheet-decision-trees-terminology-c37ee6cb2d2e