DeepAR——通过深度学习掌握时间序列预测

几年前，时间序列模型只适用于一个序列。

因此，如果我们有多个时间序列，一个选项是为每个序列创建一个模型。或者，如果我们能够将数据“表格化”，我们就可以应用梯度增强的树模型——即使在今天也能有很大的作用。

第一个可以在多个时间序列上运行的模型是DeepAR[2]，这是亚马逊开发的自回归递归网络。

在本文中，我们将了解DeepAR是如何深入工作的，以及为什么它是时间序列社区的里程碑。如果你想了解更多关于机器学习的相关内容，可以阅读以下这些文章：
哪些特征工程技术改善了机器学习预测？
以数据科学家或机器学习工程师的身份逐步构建数据管道
用合成数据创建机器学习欺诈模型
一文了解机器学习中的F1分数（F1 Score）

什么是DeepAR？DeepAR是第一个将深度学习与传统概率预测相结合的成功模型。

我们来看看DeepAR脱颖而出的原因：

• 多时间序列支持：该模型基于多个时间序列进行训练，学习全局特征，从而进一步提高预测精度。
• 额外的协变量：DeepAR允许额外的特性（协变量）。例如，如果你的任务是温度预测，你可以包括湿度水平、气压等。
• 概率输出：该模型利用分位数损失来输出预测区间，而不是进行单个的预测。
• “冷”预测：通过从数千个可能有一些相似之处的时间序列中的学习，DeepAR可以为几乎没有或根本没有历史的时间序列提供预测。

DeepAR中的LSTMS

DeepAR使用LSTM网络创建概率输出。

长短期记忆网络（LSTMS）用于许多时间序列预测模型架构：例如，我们可以使用：

• Plain LSTMs
• Multi-stacked LSTMs
• LSTMs with CNNs
• LSTMs with Time2Vec
• LSTMs in encoder-decoder topology
• LSTMs in encoder-decoder topology with attention [3] (图1)

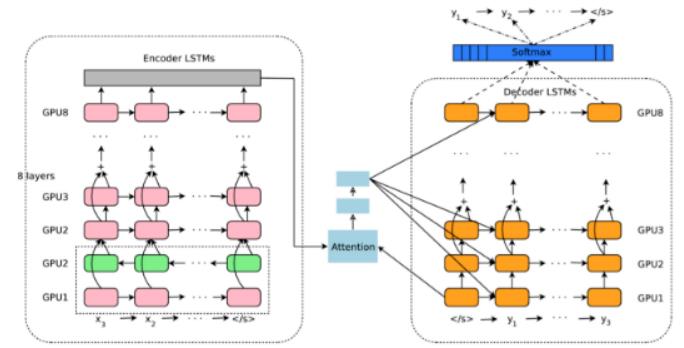
此外，虽然Transformer确实在NLP领域占据主导地位，但它们在时间序列相关任务方面并没有决定性地优于LSTM。主要原因是LSTM更擅长处理本地时间数据。

有关递归网络与Transformer的更多信息，请查看原文（https://towardsdatascience.com/towards-data-science/deep-learning-no-lstms-are-not-dead-20217553b87a）。

DeepAR-架构

DeepAR-架构与之前的模型不同，DeepAR使用LSTM的方式有点不同：

DeepAR不使用LSTM直接计算预测，而是利用LSTM参数化高斯似然函数。也就是说，估计高斯函数的θ=（μ，σ）参数（平均值和标准偏差）。

图2和图3显示了训练和推理模式下DeepAR的架构概述：

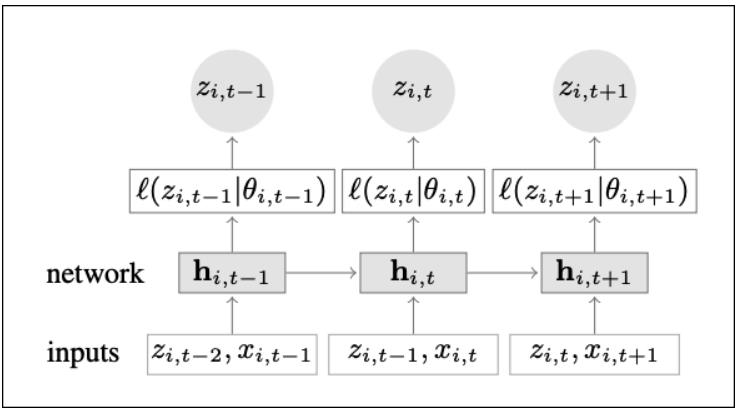
我们从训练开始。假设我们处于时间序列i的时间步长t：

1. 首先，LSTM单元将当前时间步长t的协变量x_i，t和前一时间步长t-1的目标变量z_i，t-1作为输入。此外，LSTM接收前一时间步骤的隐藏状态hi，t-1。
2. 然后，LSTM单元输出其隐藏状态hi，t，将其送入到下一步骤。
3. μ和σ值由hi，t间接计算，并“成为”高斯似然函数p（y_i|θ_i）=l（z_i，t|Θι，t）的参数。本文用希腊字母θθ=（μ，σ）定义了这些参数。如果你不理解这一部分，请不要担心，我们将在稍后详细解释。
4. 换句话说，该模型试图回答这个问题：构造高斯分布的最佳参数μ和σ是什么，该高斯分布输出的预测又是如何尽可能接近目标变量z_i，t的？
5. 训练步骤t到此结束。当前目标值z_i和隐藏状态hi，t被传递到下一时间步骤，并且训练过程继续。由于DeepAR每次训练（和预测）到一个数据点，因此该模型被称为自回归式模型。

推理步骤几乎相同。

但有一件事发生了变化：现在，在每个推断步骤t，我们使用在前一个时间步骤t-1中采样的预测变量ž_i，t-1来计算新的预测ž_i，t。

记住，ž_i，t现在是从我们的模型在训练期间学习的高斯分布中采样的。然而，我们的模型没有直接学习参数μ和σ。

我们将在下一节中了解如何计算这些参数。

高斯概似

在深入研究DeepAR的自回归性质如何工作之前，了解似然函数是如何工作的非常重要。如果你熟悉这个概念，可以跳过本节。

最大似然估计的目标是找到更好地解释样本数据分布的最佳参数。

让我们假设我们的数据遵循高斯（正态）分布。每个高斯分布由平均值μ和标准偏差σ参数化，即θ=（μ，σ）。因此，高斯似然ℓ, 给定θ=（μ，σ）定义为：

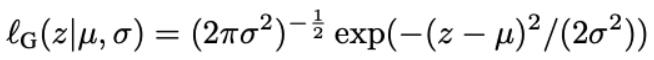
现在，看图4：

我们有绿色和橙色数据点，每个数据点都遵循不同的高斯分布。假设你得到了这些数据点，你的目标就是估计它们的两个高斯分布。

更正式地说，任务就是找到两个分布中最适合这些数据的μ和σ（DeepAR假设只有一个分布）。在统计学中，此任务也称为最大化高斯对数似然函数：

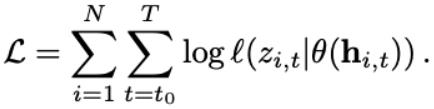
该函数在所有时间步长t都最大化⋹[t…τmax]和i⋹[1…N]，其中N是数据集中时间序列的总数。

参数估计

在统计学中，通常使用MLE公式（最大对数似然估计量）来估计参数μ和σ，MLE公式是通过对似然函数进行微分得到的。

我们不会这么做。

相反，我们让LSTM和2个密集层基于模型的输入导出这些参数。该过程如图5所示：

μ和σ估计过程很简单：

• 首先，LSTM计算其隐藏状态hi，t。
• 然后，hi，t穿过致密层W_μ来计算平均μ。
• 同样，相同的hi，t穿过第二致密层W_σ并计算平均σ。
• 现在我们有μ和σ。该模型使用这些参数创建高斯分布并进行采样。然后，模型检查该样本与实际观测值z_i，t的接近程度。
• 这就结束了时间步骤t的训练。LSTM权重和2个密集层W_。

换句话说，DeepAR通过hi、t、W_μ和W_σ间接计算μ和σ。这样做是为了通过反向传播使其计算成为可能。

在推断过程中，我们没有可供比较的目标变量z_i，t。DeepAR已经学习了所有神经网络权重，并使用它们来创建预测ž_i，t。

就是这样！我们现在已经看到了DeepAR是如何端到端工作的。

在接下来的章节中，我们将解释更多DeepAR的机制。

注：估计平均值和标准偏差参数在统计学中用μhat和σhat表示。

自动缩放

处理多个异构时间序列是很棘手的。

设想一个产品销售预测场景：一种产品的销售额可能在数百个量级，而另一种产品可能在数百万个量级。

不同量级的时间序列之间的巨大差异可能会混淆模型。为了克服这个问题，DeepAR引入了一种自动缩放机制。更具体地说，该模型计算项目相关ν_ι，以重新缩放自回归输入z_i，t。这由以下公式得出：

因此，在每个时间步骤t，来自前一步骤的自回归输入z_i，t首先被该因子缩放。

注：DeepAR的自动缩放机制工作得很好。然而，在实践中，最好先手动规范时间序列。这样做才能提高模型的性能。

时间序列中的DeepAR

在本节中，我们将讨论DeepAR如何与其他模型竞争以及其局限性。

统计模型

作者表明，DeepAR优于ARIMA这类传统统计方法。此外，与这些模型相比，DeepAR的巨大优势在于它不需要额外的特征预处理（例如，首先使时间序列稳定）。

亚马逊后来发布了一个名为DeepVAR[4]的更新版本，该版本显著提高了性能。我们将在以后的文章中描述这个模型。

深度学习模型

自从DeepAR发布以来，研究界已经发布了许多用于时间序列预测的深度学习模型。

并非所有的模型都可以直接与DeepAR进行比较，因为它们的工作方式不同。据我所知，我能想到的最接近的就是Temporal Fusion Transformer（TFT）[5]。

我们讨论一下DeepAR和TFT之间的两个显著差异：

1. 多时间序列

DeepAR为每个时间序列计算单独的嵌入。然后，这种嵌入被用作LSTM的特征，并帮助DeepAR区分不同的时间序列。

TFT也使用LSTM，工作原理类似。然而，TFT使用这些嵌入来配置LSTM的初始隐藏状态h_0。这种方法要好得多，因为TFT在每个时间序列上适当地调节LSTM单元，而不改变时间动态。

2. 预测TFT的类型

TFT不是一个自回归模型——它被归类为多水平预测模型。这两种类型的模型都可以输出多步预测。然而，多水平预测模型一次性生成预测，而不是像自回归模型那样逐个提供预测。

这种方法的优点是，多水平预测模型可以为其协方差没有任何值的时间步长创建预测。TFT在这一领域表现出色，因为它是功能多样性最强的机型之一。

结束语

DeepAR是一个卓越的深度学习模型，对时间序列社区来说是一个里程碑。

此外，这种模型在生产中很流行：它是亚马逊GluonTS[6]时间序列预测工具包的一部分，可以在亚马逊SageMaker上进行训练。

感谢阅读！你还可以订阅我们的YouTube频道，观看大量大数据行业相关公开课：https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ；在LinkedIn上关注我们，扩展你的人际网络！https://www.linkedin.com/company/dataapplab/

参考文献

[1] Created with Stable Diffusion, CreativeML Open RAIL-M license. Text prompt: “a nebula traveling through space, digital art, illustration”

[2] D. Salinas et al. DeepAR: Probabilistic forecasting with autoregressive recurrent networks, International Journal of Forecasting (2019).(https://arxiv.org/pdf/1704.04110.pdf)

[3] Yonghui Wu et al. Google’s Neural Machine Translation System: Bridging the Gap between Human and Machine Translation (2016)(https://arxiv.org/abs/1609.08144)

[4] D. Salinas et al. High-Dimensional Multivariate Forecasting with Low-Rank Gaussian Copula Processes, International Journal of Forecasting (2019).(https://arxiv.org/pdf/1910.03002.pdf)

[5] Bryan Lim et al. Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting (International Journal of Forecasting December 2021)(https://arxiv.org/pdf/1912.09363.pdf)

[6] The GluonTS package by Amazon, https://ts.gluon.ai/stable/api/gluonts/gluonts.model.deepar.html(https://ts.gluon.ai/stable/api/gluonts/gluonts.model.deepar.html)

原文作者：Nikos Kafritsas
翻译作者：王文龙
美工编辑：过儿
校对审稿：Chuang
原文链接：https://towardsdatascience.com/deepar-mastering-time-series-forecasting-with-deep-learning-bc717771ce85