从头开始实现Naive Bayesian朴素贝叶斯

我不喜欢“黑盒子”这种概念。我非常想知道东西内部的运行原理，了解这方面知识，并做出调整，即使有预备的解决方案，我也想自己编写代码看看。这正是我们在这篇文章中要做的。 

在下面的章节中，我们将使用Python和NumPy一步一步地从零开始实现朴素贝叶斯分类器（Naive Bayes Classifier）。如果你想了解更多数据分析相关内容，可以阅读以下这些文章：
想了解AB测试？重要概念合集就在这里！
10种 Regression 回归分析的方法, 到底该用哪个？
15本学习Data Mining的最佳书籍，你看过几本？
CS转行Data Science，这里是你需要的全部资源

但是，在我们开始编程之前，让我们先简要了解朴素贝叶斯分类器的理论背景及假设。

  朴素贝叶斯理论（Naive Bayes Quick Theory）

朴素贝叶斯分类器的基本原理是贝叶斯定理（Bayes’ Theorem），也因此得名。在本文示例中，我们可以将贝叶斯定理表述如下：

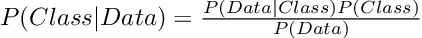
我们的总体目标，是用给定的数据去预测类（Class）的条件概率。这种概率也可以称为后验信念（Posterior Belief）。那么要如何计算后验呢？

首先，我们需要确定数据属于某个类分布 P(Data|Class)的概率。然后，我们需要将其乘以先前的 P(Class)。为了计算先验，我们需要计算特定类别的样本（行）数，然后除以数据集中的总样本数。

注意：为了简化运算，我们可以省略分母，因为 P(Data) 可以被视为标准化常数。但是，我们将不再收到从0到1的概率的分数。 

那么你可能会问，朴素贝叶斯“朴素”在哪里？

朴素贝叶斯的一个重要假设是特征的独立性。这意味着，事件A的发生不会影响事件B的发生。因此，特征之间的所有交互性和相关性将被忽略。在这个大前提下，我们现在可以在通过乘法规则计算具有多个特征的类的概率。

以上就是我们想从头开始实现朴素贝叶斯分类器所需要了解的所有内容。

  总体概述

我们已经简单了解了理论背景，现在我们来看看如何实现朴素贝叶斯。这为我们提供了更高层次的概述，我们可以将其用作某种蓝图。

• 1. 拟合（Fit）：计算（训练）数据集中每个类的汇总统计量和先验
• 2. 预测（Predict）：计算（测试）数据集中每个样本的类概率，得到给定类的（高斯Gaussian）分布的数据概率，并将其与先验相结合。

下面，我们将只实现一个类。我们将在下一节中逐步完成代码的框架，具体操作如下所示。

class NaiveBayes:
    def fit(self, X, y):
        pass
 
    def predict(self, X):
        pass

    def get_class_probability(self, x):
        pass

    def gaussian_density(self, x, mean, var):
        pass

从头开始实现

  拟合数据

正如先前的概述所述的，我们需要计算每个类（和特征）以及先验的汇总统计量。

首先，我们需要收集有关数据集的一些基本信息，并创建三个零矩阵，存储每个类的均值、方差和先验。

class NaiveBayes:
    def fit(self, X, y):
        # get number of samples (rows) and features (columns)
        self.n_samples, self.n_features = X.shape
        # get number of uniques classes
        self.n_classes = len(np.unique(y))
        
        # create three zero-matrices to store summary stats & prior
        self.mean = np.zeros((self.n_classes, self.n_features))
        self.variance = np.zeros((self.n_classes, self.n_features))
        self.priors = np.zeros(self.n_classes)

接着，我们迭代所有类，计算统计数据，并更新对应零矩阵。

class NaiveBayes:
    def fit(self, X, y):
        # ...

        for c in range(self.n_classes):
            # create a subset of data for the specific class 'c'
            X_c = X[y == c]
            
            # calculate statistics and update zero-matrices, rows=classes, cols=features
            self.mean[c, :] = np.mean(X_c, axis=0)
            self.variance[c, :] = np.var(X_c, axis=0)
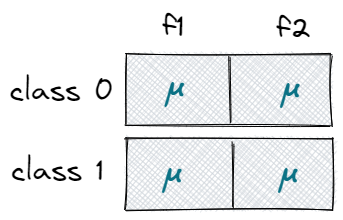
            self.priors[c] = X_c.shape[0] / self.n_samples

例如，假设我们的数据集中有两个唯一的类 (0,1) 和两个特征。因此，存储平均值的矩阵将具有两行两列 (2×2)。每个类占一行，每个特征占一列。

先验是单一向量 (1×2)，是单个类的样本除以总样本容量的比例。

  预测

这个部分会稍微复杂一些……

为了做出预测，我们需要得到数据属于哪一类，或更具体地说，来自同一分布的概率。

为了方便起见，我们假设数据的基础分布是高斯分布。我们创建一个类方法，其返回新样本的概率。

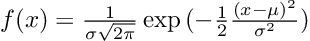
class NaiveBayes:
    #...
    def gaussian_density(self, x, mean, var):
        # implementation of gaussian density function
        const = 1 / np.sqrt(var * 2 * np.pi)
        proba = np.exp(-0.5 * ((x - mean) ** 2 / var))
    return const * proba

这种方法接收单个样本并计算概率。但是，从参数中可以看出，我们还需要提供均值和方差。

因此，我们创建了另一个类方法。这个方法可以迭代所有类，收集汇总统计信息、先验信息，并计算单个样本的新后验信念。

class NaiveBayes:
    #...
    def get_class_probability(self, x):
        # store new posteriors for each class in a single list
        posteriors = list()

        for c in range(self.n_classes):
            # get summary stats & prior
            mean = self.mean[c]
            variance = self.variance[c]
            prior = np.log(self.priors[c])
            
            # calculate new posterior & append to list
            posterior = np.sum(np.log(self.gaussian_density(x, mean, variance)))
            posterior = prior + posterior
            posteriors.append(posterior)
        
        # return the index with the highest class probability
        return np.argmax(posteriors)

请注意，我们在这里应用对数转换（Log-transformation），通过增加概率简化计算。我们还会返回具有最高后验置信度（posterior belief）的类索引。

 class NaiveBayes:
        #...
    def predict(self, X):
        # for each sample x in the dataset X
        y_hat = [self.get_class_probability(x) for x in X]
        return np.array(y_hat)

最后，我们可以将其与预测方法结合在一起。

  测试分类器

现在，我们完成了朴素贝叶斯分类器，只剩最后一件事——测试分类器。

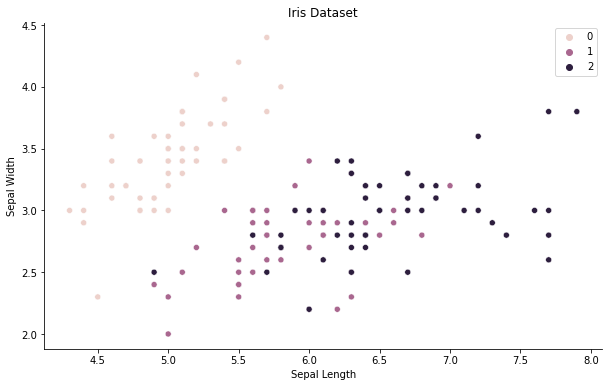
我们将使用鸢尾花（iris）数据集，该数据集由 150 个样本组成，具有 4 个不同的特征（萼片长度、萼片宽度、花瓣长度、花瓣宽度）。我们的目标是在 3 种不同类型的鸢尾花中预测正确类别。

from sklearn import datasets
from sklearn.model_selection import train_test_split

# load iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target

# split into train and test data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)

# instantiate, train and predict Naive Bayes Classifier
nb = NaiveBayes()
nb.fit(X_train, y_train)
predictions = nb.predict(X_test)

# helper function to calculate accuracy
def get_accuracy(y_true, y_hat):
    return np.sum(y_true==y_hat) / len(y_true)
  
# print results
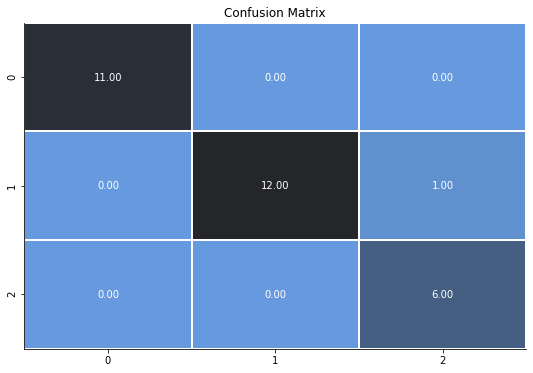
print('Naive Bayes Accuracy: ', get_accuracy(y_test, predictions))

通过运行上述代码，我们加载并准备鸢尾花数据集，从而训练分类器。在对测试数据进行预测时，准确率高达96.6% 。

下面的混淆矩阵告诉我们，我们的分类器犯了一个错误，将第一类错误地分类为第二类。

  结论

在本文中，我们使用了 Python 和 NumPy 从头开始实现了朴素贝叶斯分类器。我们了解了理论背景，并亲手运用了这个理论。

如果你像我一样，希望完全了解算法的逻辑，那么从头开始实现朴素贝叶斯是深入了解其内部运行原理的最佳方法之一。

感谢您的阅读！你还可以订阅我们的YouTube频道，观看大量数据科学相关公开课：https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ；在LinkedIn上关注我们，扩展你的人际网络！https://www.linkedin.com/company/dataapplab/

原文作者：Marvin Lanhenke
翻译作者：Lia
美工编辑：过儿
校对审稿：Jiawei Tong
原文链接：https://towardsdatascience.com/implementing-naive-bayes-from-scratch-df5572e042ac