
Huber回归和Ridge回归:如何处理Python中的异常值?
在处理数据中的异常值时,传统的线性回归可能存在一些缺点。
具体来说,如果一个数据点离集合中的其他点很远,这会极大地影响最小二乘回归线(least squares regression line),意思是,接近集合数据点的总体方向的线将因异常值的存在而发生偏移。

为了防止出现这种情况,我们可以使用对异常值具有鲁棒性的修正回归模型。在本例中,我们主要分析 Huber 和 Ridge 回归模型。如果你想了解更多数据分析相关内容,可以阅读以下这些文章:
使用 PySpark 和 MLlib 构建线性回归预测波士顿房价
随机森林回归的一个局限
10种 Regression 回归分析的方法, 到底该用哪个?
让科学回归到数据科学中——Daniel Whitenack
背景
本例中使用的数据集是皮马印第安人糖尿病数据集(Pima Indians Diabetes)数据集,该数据集最初来源于国家糖尿病、消化和肾脏疾病研究所(the National Institute of Diabetes and Digestive and Kidney Diseases),由 CC0 1.0 通用(CC0 1.0)公共领域贡献许可证(CC0 1.0 Universal Public Domain Dedication)提供。
在本例中,我们需要建立一个回归模型,来预测患者的体重指数 (BMI) 水平。
在看 BMI 的箱形图时,通过图表上半部分的数据点,我们可以看到数据集中存在明显的异常值。
# Creating plot
plt.boxplot(bmi)
plt.ylabel("BMI")
plt.title("Body Mass Index")
# show plot
plt.show()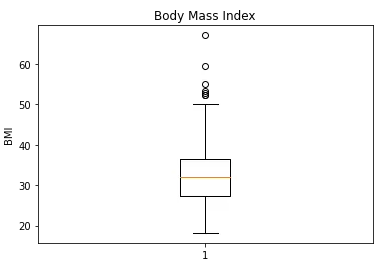
然后,我们需要跨数据创建相关系数矩阵(Correlation Matrix):
corr = a.corr()
corr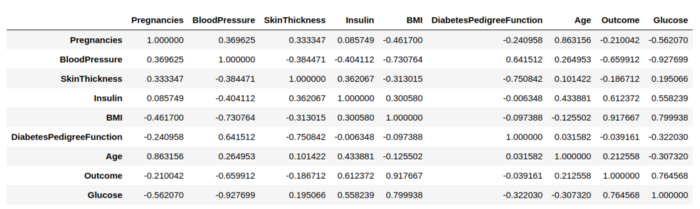
下图是使用 seaborn 的视觉效果:
sns.heatmap(a.corr());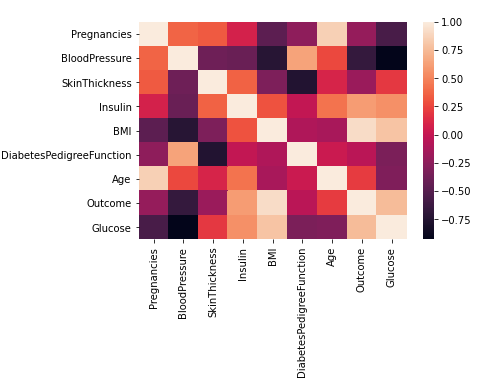
线性回归分析(Line Regression Analysis)
在自变量中,我们选择皮肤厚度(Skin Thickness)和葡萄糖(Glucose),假设这两个变量对 BMI 有显着影响。
然后对样本数据生成回归,结果如下:
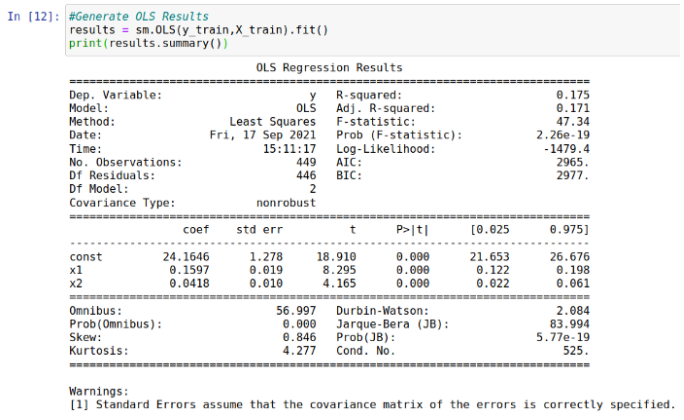
根据以上结果显示:
- 在保持所有其他变量不变的情况下,皮肤厚度增加1个单位,会导致BMI增加0.159。
- 在保持所有其他变量不变的情况下,葡萄糖水平增加1个单位,会导致BMI增加0.0418。
我们看到,这两个变量的变化都非常显着(假设 p 值为 0)。虽然 17.5% 的拟合度(R-Squared) 很低,但这并不一定意味着我们的模型有问题。鉴于有很多变量可以影响 BMI 的波动——这只能表明,该模型没有考虑到这些变量。然而,结果显示,本例中使用的两个自变量的联系十分紧密。
我们根据验证的数据集生成预测,并计算均方根误差 (RMSE) 值。在本例中,我们用RMSE作为判断标准。因为RMSE值对异常值更敏感。RMSE越高,预测的误差就越大。
>>> olspredictions = results.predict(X_val)
>>> print(olspredictions)
[36.32534071 31.09716546 28.67493585 34.29867119 35.03070074
...
36.50971909 35.97416079 36.57591618 35.10923948 34.3672371]计算出均方根误差(RMSE):
>>> mean_squared_error(y_val, olspredictions)
>>> math.sqrt(mean_squared_error(y_val, olspredictions))
5.830559762277098
>>> np.mean(y_val)
31.809333333333342相对于整个验证集的平均值——31.81,均方根误差的值为 5.83。
接下来,我们要生成 Huber 和 Ridge 回归模型。以同样的方式,通过使用这些回归模型,对验证集进行预测,并计算均方根误差。
Huber vs. Ridge
Huber 和 Ridge 回归模型的目的都是生成一条回归线,与标准线性回归相比,该回归线对异常值的敏感度较低。
但是,这些模型的运行方式略有不同。
具体来说,Huber 回归模型取决于 M 估计(M-estimate),与均值相比,测量对异常值敏感度更低的位置(该理论基于《牛津统计词典》(厄普顿和库克,2014 年))。
而岭回归模型(Ridge Regression)使用 L2 正则化——这使得异常值的权重更小,从而对回归线的影响更小。此外,L2 还会正则化估计数据的均值,避免过度拟合,而 L1 正则化(在Lasso回归中使用)会估计数据的中位数。
在本例中,我们使用 Huber 和 Ridge 回归模型进行预测,计算根据验证集生成的预测评价指标RMSE;并根据验证集,计算预测的 RMSE。然后使用效果最好的模型,对整个测试集进行预测。
Huber 回归(Huber Regression)
以下为Huber 回归模型示例:
hb1 = linear_model.HuberRegressor(epsilon=1.1, max_iter=100, alpha=0.0001, warm_start=False, fit_intercept=True, tol=1e-05)特别需要说明的是,epsilon值测量的是应该被归类为异常值的样本数。该值越小,模型对异常值的鲁棒性越强。
从这个角度来看,我们得出5个具有不同 epsilon 值的 Huber 回归模型。
hb1 = linear_model.HuberRegressor(epsilon=1.1, max_iter=100, alpha=0.0001, warm_start=False, fit_intercept=True, tol=1e-05)
hb2 = linear_model.HuberRegressor(epsilon=1.8, max_iter=1000, alpha=0.0001, warm_start=False, fit_intercept=True, tol=1e-05)
hb3 = linear_model.HuberRegressor(epsilon=2.5, max_iter=1000, alpha=0.0001, warm_start=False, fit_intercept=True, tol=1e-05)
hb4 = linear_model.HuberRegressor(epsilon=3.2, max_iter=1000, alpha=0.0001, warm_start=False, fit_intercept=True, tol=1e-05)
hb5 = linear_model.HuberRegressor(epsilon=3.9, max_iter=1000, alpha=0.0001, warm_start=False, fit_intercept=True, tol=1e-05)根据验证集对五个模型进行了预测。以第一个模型为例:
>>> hubermodel1 = hb1.fit(X_train,y_train)
>>> huberpredictions1 = hb1.predict(X_val)
>>> print(huberpredictions1)
[35.67051275 29.43501067 27.18925225 33.91769821 34.47019359
...
31.52694684 31.0940833 35.37464065 30.99181107 36.11032014]计算得到的均方误差如下:
- hb1 = 5.803
- hb2 = 5.800
- hb3 = 5.816
- hb4 = 5.825
- hb5 = 5.828
可以看到, 这里的RMSE 值都略小于使用 OLS 回归模型时计算得到的 5.83。hb2 或 epsilon 值为 1.8 的模型的效果最好——尽管差距不大。
岭回归(Ridge Regression)
跟刚刚一样,我们使用岭回归模型进行预测,然后计算 RMSE:
>>> rg = Ridge(fit_intercept=True, alpha=0.0, random_state=0, normalize=True)
>>> ridgemodel = rg.fit(X_train,y_train)
>>> ridgepredictions = rg.predict(X_val)
[36.32534071 31.09716546 28.67493585 34.29867119 35.03070074
...
31.79765405 36.18771132 31.86883756 36.98120033 35.68182273]均方误差实际上与使用 OLS 回归计算的结果相同:
>>> mean_squared_error(y_val, ridgepredictions)
>>> math.sqrt(mean_squared_error(y_val, ridgepredictions))
5.8305针对测试集的效果
鉴于 epsilon= 1.8 的 Huber 回归模型对验证集的效果最好(尽管差距不大),让我们看看它在测试集上的效果如何。
在这种情况下,皮马印第安人糖尿病数据集(Pima Indians Diabetes)的一部分与其余数据表面上分隔来开——检查模型在不可见数据中的效果。
以下是预测结果:
>>> btest = t_bmi
>>> btest=btest.values
>>> bpred = hb2.predict(atest)
>>> bpred
array([33.14957023, 30.36001456, 32.93500157, 28.91518701,
...
34.72666166,36.29947658, 39.13505914, 33.77051646])计算出的测试集RMSE 和平均值:
>>> math.sqrt(mean_squared_error(btest, bpred))
5.744712507435319
>>> np.mean(btest)
32.82418300653595由于 RMSE 值仅占平均值的 17% 以上——该模型在预测整个测试集的 BMI 值方面效果非常好。
正如我们所看到的,所有模型的 RMSE 值或多或少是相似的——Huber 回归模型提供的 RMSE 值略低。但是,根据异常值的大小,在某些情况下,Huber 和 Ridge 回归模型的效果明显比OLS好。
结论
在本例中,你已经看到:
- 如何直观地找到数据样本中的异常值
- Huber 回归和 Ridge 回归的区别
- 如何在 Huber 回归中修改异常值敏感度
- 使用 RMSE 确定模型精度
感谢你阅读这篇文章,也欢迎你提出问题或提供反馈。你还可以订阅我们的YouTube频道,观看大量数据科学相关公开课:https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ;在LinkedIn上关注我们,扩展你的人际网络!https://www.linkedin.com/company/dataapplab/
原文作者:Michael Grogan
翻译作者:Lia
美工编辑:过儿
校对审稿:Jiawei Tong
原文链接:https://towardsdatascience.com/huber-and-ridge-regressions-in-python-dealing-with-outliers-dc4fc0ac32e4


