每个数据科学家都应该知道的关于回归的三个简单的事情

理解这三件事将改善你如何进行线性和广义线性建模。如果你想了解更多关于回归的相关内容，可以阅读以下这些文章：
关于线性回归：一个关键且经常被误解的事实
Python的自回归分布滞后模型简介
逻辑回归问题，你解释到点子上了吗？
Correlation相关性 VS Regression回归：它们有什么区别？

我认为自己更像是一个数学家，而不是数据科学家。我不能让自己盲目地执行方法，而不了解底层发生了什么。我必须深入研究数学才能相信结果。这是一件好事，因为现在很容易运行模型，然后下班回家。

一个模型的好坏取决于你对它的理解，我担心很多人在运行模型时，只接受从模型中得出的第一个结果。说到回归建模(最常见的建模形式之一)，如果你能理解这些模型是如何工作的，以及为什么它们是以这种方式建立的，你就会成为一名更好的数据科学家。

01# 你是在预测一个平均值，而不是一个实际值

当你运行一个回归模型时，通常你会发现输入变量和与结果相关的某种平均值之间的关系。我们来看看线性回归。当我们进行线性回归时我们对结果变量y做了两个非常重要的假设。

• 任意输入变量y的可能值都分布在均值附近。
• y的均值与输入变量呈相加关系。也就是说，要得到y的均值，你需要将一些依赖于每个输入变量的数字加起来。

当你使用模型进行预测时，对于给定的一组输入值，y的预测(或建模)值是y可能取的所有可能值的平均值的估计值。因此，在沟通模型的结果时，你应该始终小心确保这种不确定性是清楚的。

一种方法是使用预测区间，它假设y在模型均值周围呈正态分布。请注意，这与通常由模型产生的置信区间不同，置信区间只是平均值周围的不确定性区间，因此通常比预测区间窄得多。在下面的图表中，我展示了日本第一次樱花盛开的日期与3月份的平均温度相关的拟合线性回归。红线表示模型均值，深灰色区域表示该均值附近的置信度，浅蓝色区域表示95%的预测区间。看到这有多宽了吗？它应该是，因为它试图捕捉95%可能的y值。

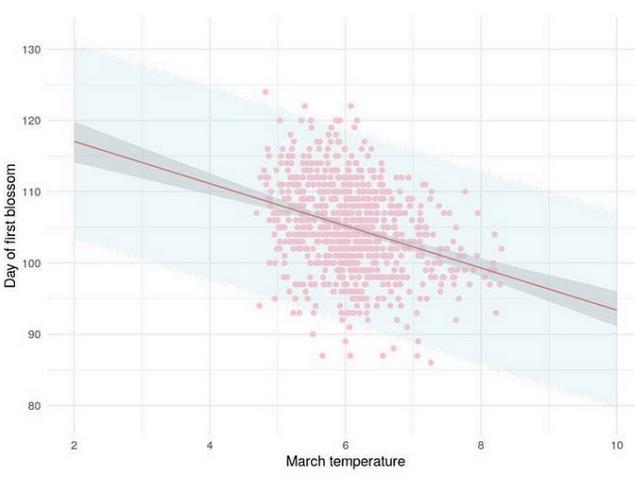
链接到这个图像的R代码，（https://gist.github.com/keithmcnulty/b5c99be9185ef18e6925512e2b24ec63）

考虑上图的一种方法是考虑三月温度任意给定值的垂直“切片”。这个切片可以被认为是一个“隐藏的钟形曲线”。中心的红点代表钟形曲线的预期中心，深灰色区域代表钟形曲线中心周围95%的不确定性范围，浅蓝色阴影区域代表整个钟形曲线的95%。

02# 对预测结果有一个正态分布的期望

可以帮助检查模型的质量

在线性回归中，考虑你的结果是否在模型均值周围呈正态分布是很有帮助的。这意味着，如果你把模型的所有误差——或残差——绘制在直方图上，它们看起来更像钟形曲线吗？如果残差分布基本上不是正态分布，那么这可能表明一个更准确或更有效的模型隐藏在某个地方等待被发现。

你可以用这个指标来衡量你的模型有多“好”。你的误差分布看起来越“正态”，你就越有信心你所建模的均值是一个“好的”均值，你对你的参数也就越有信心。所以在你运行了一个线性模型之后，我发现检查残差的分布是个好主意。你可以使用简单的直方图或密度图来做到这一点。或者你可以使用分位数-分位数图(或QQ图)。QQ图将模拟结果的分位数与完美正态分布的理论分位数进行比较。这条线越完美，你就越有信心你的模型是一个“好的”均值。

在下面的例子中，我建立了一组人的身高和体重之间的关系模型，其中一些是儿童。在左边，我建立了身高和体重之间的直接线性模型，在右边，我建立了身高和体重对数之间的线性关系模型。上面一行为模型拟合，中间一行为残差分布，下面一行为相应的q -plot。你可以看到，在右手边，我们的模型对高度的平均值做出了更好的估计。

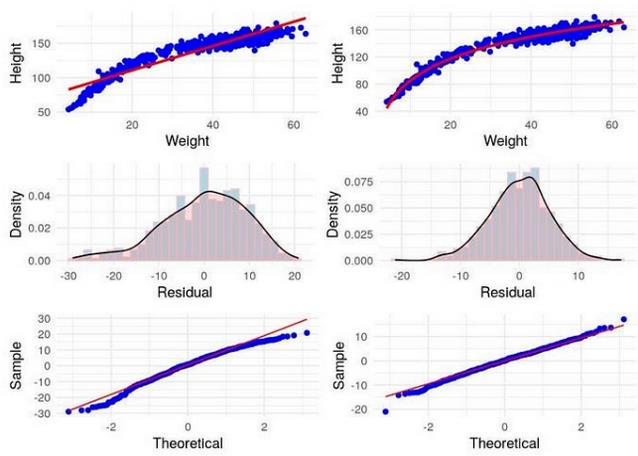
链接到这个图像的R代码（https://gist.github.com/keithmcnulty/0f2dd5967938e913fa8ca76bac9b5a08）

03# 当你的过程是乘法时，你必须做一个重要的转换

上面的两个例子演示了我们通常期望从加法过程中得到什么，这是什么意思呢？

在线性建模中，我们通过添加一堆东西来对我们的结果进行建模——这些“东西”通常是每个输入变量的某些倍数或变换。假设这些输入变量中的每一个本质上都是随机的，当你创建随机变量的线性组合时，你期望在一个足够重复的样本中看到正态分布。为了说明这一点，我对0到1之间的10个随机数求和10,000次，下图显示了结果的直方图和密度图。明白我的意思吗？

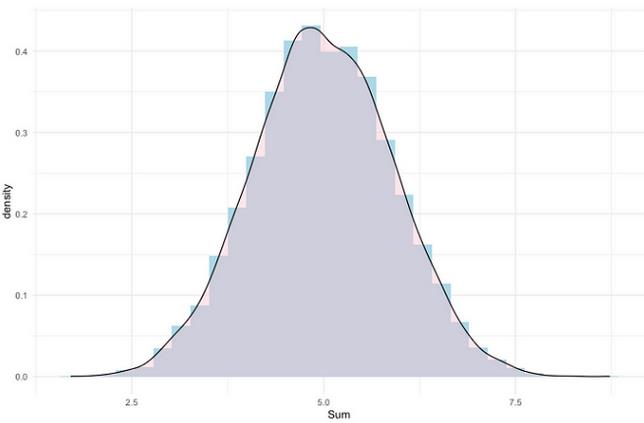
链接到这个图像的R代码，（https://gist.github.com/keithmcnulty/b1dce511bc1611cbf0220dbd734a27ec）

对于加法过程来说，这一切都很好。但是当你的过程变成乘法时，事情就变了。

当你为概率或赔率建模时，你是在为一个基本的乘法过程建模——输入变量被认为对结果的赔率或概率有乘法效应。

现在，当我在1到2之间随机选择10个数字并将它们相乘会发生什么？经过10000次测试，我得到了这样的分布：

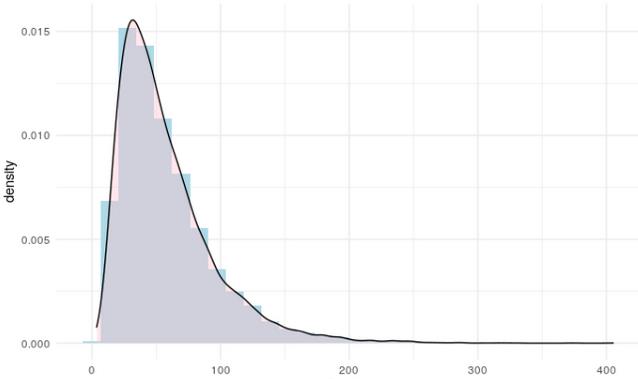
链接到这个图像的R代码（https://gist.github.com/keithmcnulty/93f21b1e7203bdc342145986b7daa3ba）

我们有麻烦了。这个分布不是正态分布，所以我们所有的线性回归方法现在都失效了。

可是等等。有没有一种方法可以将我们的结果变量转化为一个累加过程的结果?还记得高中的指数规则吗?或者换一种说法，对数规则：log(ab)=log(a) + log(b)。所以乘法过程的对数就是加法过程！

让我们通过查看前面图表中乘积的对数分布来验证这一点：

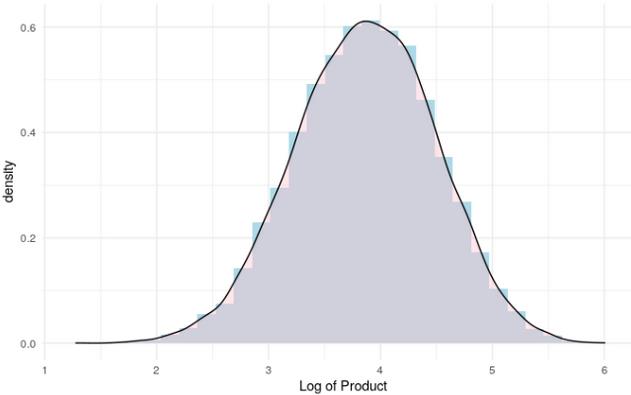
链接到这个图像的R代码（https://gist.github.com/keithmcnulty/0c3883478442118e308bf5b5a9e83b4e）

答对了！因此，我们可以通过转换为对数和使用类似线性回归的方法来模拟概率或几率等乘法过程。我们只需要记住在最后通过对所有项求幂来进行变换。这就是为什么在逻辑回归中，我们用对数概率来建模，为了得到比值比，我们对系数求幂，这就是为什么我们经常用对数正态分布来描述乘法过程的分布。

我希望你发现这些简单但重要的观察对你理解回归的基础有用。如果你认为这是有帮助的，你可能会发现我的《Handbook of Regression Modeling in People Analytics》是一个有用的资源。

我希望你发现这些简单但重要的观察对你理解回归的基础有用。你还可以订阅我们的YouTube频道，观看大量大数据行业相关公开课：https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ；在LinkedIn上关注我们，扩展你的人际网络！https://www.linkedin.com/company/dataapplab/

原文作者：Keith McNulty
翻译作者：Dou
美工编辑：过儿
校对审稿：Chuang
原文链接：https://keith-mcnulty.medium.com/three-simple-things-about-regression-that-every-data-scientist-should-know-d38ee17c5563