
查找时间序列数据中异常值的终极指南(第 1 部分)
异常值:那些会扭曲统计模型、扰乱预测并破坏决策过程的麻烦数据点。
难怪在数据分析中它们不太受欢迎。
本文是关于时间序列数据中异常值识别和管理的三部曲系列的第一部分。
在这篇初始文章中,我们将探索有效识别时间序列数据中异常值的可视化和统计方法。这些基础知识对于任何希望提高分析准确性的人来说都是至关重要的。如果你想了解更多关于时间序列的相关内容,可以阅读以下这些文章:
金融中的机器学习:利用随机森林掌握时间序列分类
关于时间序列分析(TSA),你需要知道这15个词
DeepAR——通过深度学习掌握时间序列预测
Python机器学习库:pycarets新增时间序列模块
在第二篇文章中,我将专门讨论机器学习方法,鉴于其重要性和复杂性,它们值得专门讨论。
查找时间序列数据中的异常值终极指南(第2部分)用于时间序列分析中异常值检测的有效机器学习方法和工具
然后,第三篇文章将探讨如何管理这些异常值的各种策略。我们将重点讨论转换技术,提供减轻其影响的实际解决方案。
让我们开始吧!
内容:
第I部分(本文):
- 为什么要关心?
- 异常值与异常
- 如何选择正确的异常检测方法?
- 单变量与多变量时间序列数据
- 检测数据中异常值的最佳方法是什么?
- 可视化方法
- 统计方法
6.评估指标
第II部分(此处):
3.异常值的识别
- 机器学习方法
- 评价指标
第III部分(即将发布):
4.异常值的处理
- 忽略或移除?
- 转换技术
- 插补
- 限制
为什么要关心?
如果你在阅读这篇文章,你可能知道在进行任何建模之前处理异常值是多么重要。
你应该关心时间序列数据中异常值的一些原因:
- 异常值会显著扭曲和误导数据集的关键统计数据,如均值、方差和相关系数。
- 异常值会影响预测模型的性能。
- 异常值可能掩盖时间序列数据中的真实趋势和周期性行为。
- 基于未仔细检查异常值的数据做出的决策可能导致糟糕的战略决策。
还有许多其他原因说明在时间序列数据中处理异常值对于有效分析是至关重要的,但这些理由足以激励我们开始探索。
异常值与异常
我将“异常”和“异常值”这两个术语交替使用,但它们的定义有细微差别。异常可以指任何偏离常态的数据点,而异常值具体指远离大多数数据点的极端值。许多方法可以应用于异常和异常值。
顺便说一句,我写了一篇关于我开发的新颖异常检测方法的文章,欢迎查阅!
更高级别的异常检测:解锁神经元洞察力
利用神经元的力量变革异常检测!
如何为时间序列数据选择合适的异常值检测方法?
为时间序列数据选择最佳异常检测方法首先需要对数据集和预期异常有深刻理解。
话虽如此,首先考虑数据集的大小和可用的计算资源。
对于可解释性的数据集,简单的方法如Z-Score和移动平均可能是理想的。然而,更复杂的场景,如需要检测细微模式的情况,可能受益于需要大量数据和计算能力的高级技术,如LSTM网络(将在本系列的第二部分中介绍)。
记住:数据集大小、计算资源、解释性和任务的性质是选择合适的异常值检测方法的关键。
尝试多种方法和指标来准确评估其性能可能是有益的。如果可能,考虑使用多种方法的集合来提高准确性。此外,利用你或领域专家对该领域的了解可以指导你选择方法。
没有一刀切的解决方法;最佳方法将取决于你的数据的具体特征、你希望检测的异常的性质以及你的具体需求。
在像欺诈检测这样的领域,评估异常检测方法尤其具有挑战性,因为异常很少见但意义重大。
精确率、召回率和F1分数等指标对于评估这些方法在捕捉欺诈活动并减少误报方面的效果至关重要。
在像预测性维护这样的环境中,ROC曲线和AUC指标对于及时识别潜在的机器故障非常有价值。
在医疗保健等行业中,可视化经常用于监测患者的生命体征,但这些方法的准确性在很大程度上依赖于领域专家的正确解释。
单变量与多变量数据
在开始异常值分析之前,重要的是要考虑你的数据是单变量还是多变量。
单变量时间序列数据由随时间记录的一系列单个观察值组成。典型示例包括每日股票价格、每月销售数据或年度天气数据。
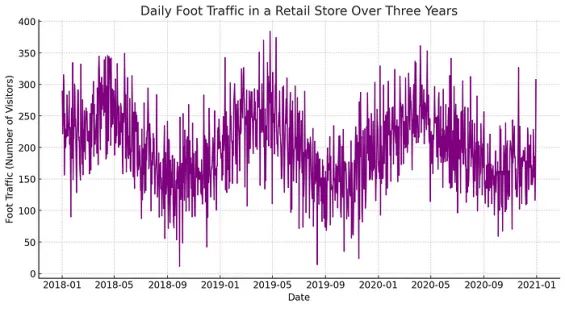
相比之下,多变量时间序列数据涉及多个变量或序列,它们在相同时间间隔内被观察和记录。
这种类型的数据捕捉了不同变量之间的关系和相互作用,以及它们各自的趋势和季节性变化。例如,多变量时间序列可以包括同时记录的每日温度、湿度和风速测量值。
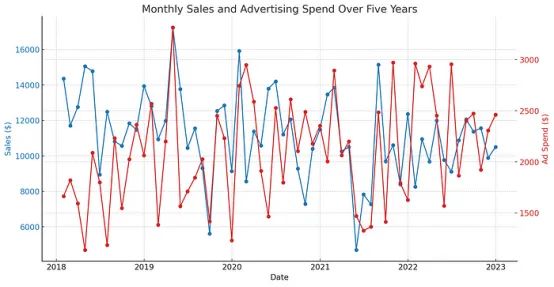
本文中描述的一些方法更适合单变量数据,而其他方法则专为处理多变量数据而设计。
然而,其中一些方法可以应用于两者。在深入探讨这些方法之前,我将在这里概述几种常见的单变量和多变量数据方法:
对于单变量数据,通常使用时间序列图和箱线图等可视化检查方法,专注于一次一个变量。STL分解传统上也用于单变量设置。对这类数据也使用Z-score、修正的Z-score方法和Grubbs检验。
机器学习方法如孤立森林(Isolation Forest)、局部异常因子(LOF)和自动编码器(Autoencoders)通常用于多变量数据的降维和异常检测,但它们也可以压缩和重构单变量时间序列数据,以根据重构误差识别异常。
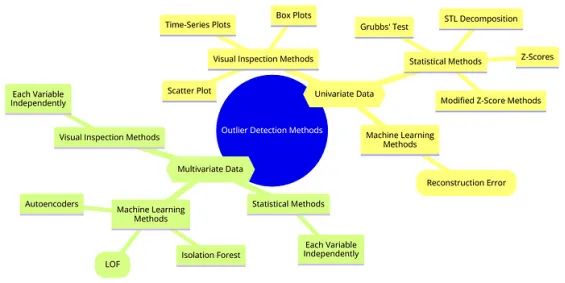
PS:异常值检测方法不止思维导图中列出的这些。
对于多变量数据,散点图分析是检验多变量关系的常用方法。孤立森林、LOF和自动编码器自然适合处理高维数据。
请注意,一些单变量方法也可以应用于多变量数据。例如,Z-score方法可以在多变量场景中独立计算每个变量的Z-score。
箱线图可以用于多变量数据集中每个变量,分别识别每个维度的异常值。在多变量场景中,可以使用散点图绘制变量对。STL分解虽然传统上用于单变量,但可以通过独立分解每个序列来适应多变量序列分析。
检测数据中异常值的最佳方法是什么?
可视化方法
可视化检查是识别时间序列数据中异常值的基本方法。数据的性质也会影响可视化检查的进行方式。
时间序列图
这是时间序列数据最直接的图表。它允许你查看趋势、模式、季节性变化及随时间变化的潜在异常值。与其他数据明显偏离的点通常很容易被发现。
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
def plot_temporal_trends(df, columns):
num_plots = len(columns)
fig, axes = plt.subplots(num_plots, 1, figsize=(10, num_plots * 3), sharex=False) # sharex=False to not share x-axis
fig.suptitle(f'Temporal Trends', fontsize=16, y=1.02 + 0.01 * num_plots)
if num_plots == 1: # Ensure axes is iterable
axes = [axes]
for ax, col in zip(axes, columns):
ax.plot(df.index, df[col], marker='o', markersize=4, linestyle='-', label=col)
ax.set_title(f'{col} - {title}')
ax.set_ylabel('Value')
# Setting the date formatter for each subplot's x-axis
ax.xaxis.set_major_locator(mdates.YearLocator(base=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y'))
# Rotate and align the tick labels so they look better
ax.tick_params(axis='x', rotation=45)
ax.legend()
plt.tight_layout(rect=[0, 0, 1, 0.97]) # Adjust layout to make room for the title
plt.show()
columns = df.columns.tolist()
plot_temporal_trends(df, columns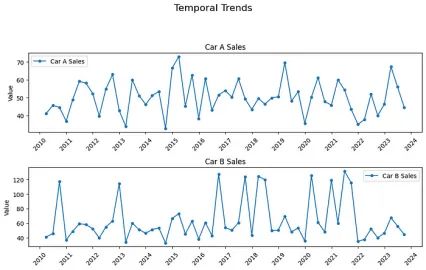
你能找到异常值吗?这种可视化可能会直接显示异常值,或者根据数据的复杂性可能需要更详细的分析。在大多数情况下,可能需要额外的可视化来确认对异常值怀疑。
异常值分析中的季节性考虑因素
按季节处理异常值非常有意义,尤其是在处理具有季节性变化的数据时。许多时间序列数据集在特定的时间段内会显示出明显的模式。
实际上,一个最初看起来是异常值的数据点在按季节处理时可能并不会被认为是异常值。同样,这取决于数据和问题的性质!
例如,我最近参与了一个涉及水库水质测量时间序列数据的项目。很明显,这些异常值需要按季节进行分析。每个季节都有其自身的特征和趋势,以独特的方式影响参数。通过按季节分段数据,我可以更有效地对每个子集应用特定的异常值检测方法。
季节性可以对数据中展示的趋势和行为产生重大影响,通过按季节分析可以提供更有见地和相关性的结论。
例如,雨季期间水质的异常值可能是由于径流而产生的典型现象,而在旱季同样的异常值可能是不寻常的。
此外,季节性分析可以通过考虑周期性的季节效应来改进预测模型。这对于受季节变化影响较大的行业,如农业、旅游业和零售业,至关重要。
箱线图
箱线图用于静态地识别数据集或数据子集内的异常值。须线外的点(通常设置在四分位数间距的1.5倍处)是潜在的异常值。
def plot_outliers(param_dfs):
for key, df in param_dfs.items():
plt.figure(figsize=(10, 6))
df.boxplot()
plt.title(f'Boxplot of {key}')
plt.xticks(rotation=45)
plt.show()
# Call the function to plot the outliers
plot_outliers(param_dfs)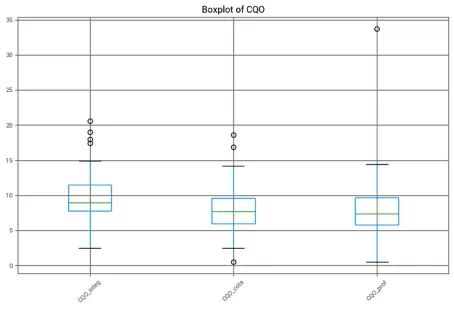
在上图中,我分析了不同水深下的特定参数,并将它们并排进行比较。图中的小黑圈代表潜在的异常值。这些视觉提示对于快速识别每个子集中明显偏离常规的数据点至关重要。
散点图
如果时间序列数据与另一个变量相关,散点图可以帮助识别两个变量背景下的异常值。
# Plotting
plt.figure(figsize=(10, 6))
# Normal data
plt.scatter(df['Annual Income'][:-5], df['Credit Card Spending'][:-5], color='blue')
plt.title('Annual Income vs Credit Card Spending')
plt.xlabel('Annual Income ($)')
plt.ylabel('Credit Card Spending ($)')
plt.legend()
plt.grid(True)
plt.show()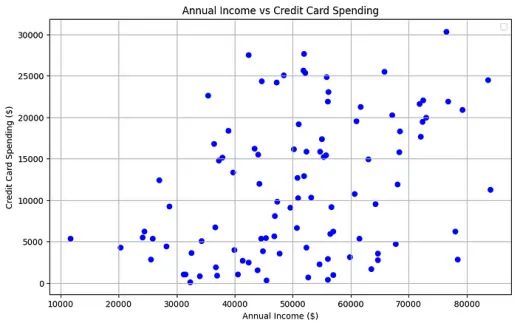
统计方法
STL分解
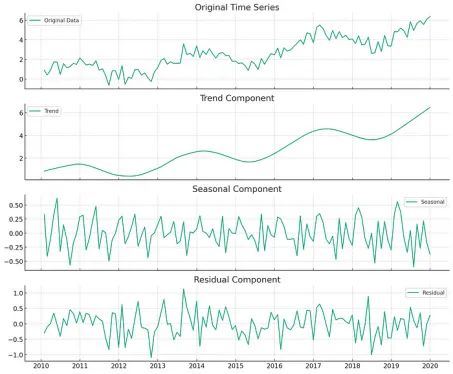
众所周知,时间序列数据可以分解为趋势、季节性和残差。
趋势是长期观察到的基本方向或模式,季节性是由于季节因素而发生的周期性波动,残差是在去除趋势和季节性成分后数据中留下的随机变动。
为此,STL分解通过LOESS(局部估计散点平滑)有效地将时间序列信号分离为这三个独立的组成部分,增强了我们根据对数据基本行为更清晰的洞察进行分析和预测的能力。
注意:STL假设数据点按时间顺序排列。STL分解期望系列数据点按其自然时间顺序依次排列。这对于准确估计趋势和季节变化至关重要,因为每个数据点都有助于理解其后续数据点的特征。
STL如何帮助你识别异常值?
STL分解的残差部分表示无法通过季节性和趋势成分解释的数据部分。
理想情况下,残差应该是随机噪声。异常值通常表现为残差序列中的异常高峰或低谷,其显著偏离典型噪声水平。因此,要寻找残差中的极端值。由于残差理想情况下代表随机噪声,任何显著的偏差可能都表示存在异常值。
通过分析残差的标准差,可以识别那些与平均残差显著不同的数据点,通常被分类为异常值。例如,距离平均残差超过2或3个标准差的数据点可以被视为异常值。
趋势成分平滑了短期波动,突显了数据集的更广泛运动。异常值可能会引起趋势的意外变化或不符合大多数数据所建立的平滑模式的突然变化。
步骤1:查看残差图
首先查看由STL分解得出的残差图。此图显示无法通过趋势或季节性成分解释的数据点。
步骤2:计算统计指标
计算残差的平均值和标准差。这将有助于确定哪些数据点与我们在正态分布噪声模式中预期的情况显著不同。
步骤3:定义异常值的阈值
通常,距离平均残差超过2或3个标准差的数据点被视为异常值。你可以根据对异常值的敏感程度选择阈值。对于许多应用程序来说,使用3个标准差是常见的选择。
步骤4:识别异常值
识别超过此阈值的残差成分中的数据点。这些是潜在的异常值。
步骤5:可视化检查和交叉验证
你可以重新查看原始时间序列图以及趋势和季节成分的图表。查看已识别的异常值在这些组成部分中的位置。
检查异常值是否可能只是不寻常但真实的变化,或者它们是否可能表明错误或异常。这可能涉及对数据的背景知识。
import numpy as np
#Example
# Calculate the mean and standard deviation of the residuals
residuals = result.resid
mean_resid = np.mean(residuals)
std_resid = np.std(residuals)
# Define a threshold for outlier detection
threshold = 3 * std_resid
# Identify potential outliers
outliers = residuals[np.abs(residuals - mean_resid) > threshold]
# Print outlier dates and values
print(outliers)Z-score和修正后的Z-score方法
Z-score,也称为标准分数,用于衡量数据点与数据集平均值之间的标准差。算公式如下:
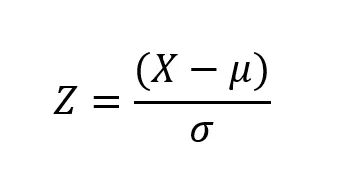
- X是单个数据点。
- μ是数据集的平均值。
- σ是数据集的标准差。
z值大于某个阈值(通常为2或3)的数据点被认为是离群异常值。
注意:Z-score方法假设数据服从正态分布或至少近似正态分布。它还假设异常值相对于平均值和标准差具有极端值。
import numpy as np
def identify_outliers_with_z_score(df, z_thresh=z_thresh):
print("Outliers using Z-score method:")
for col in df.columns:
if np.issubdtype(df[col].dtype, np.number): # Numerical data only
df_col = df[col].dropna() # Drop NaN values
z_scores = np.abs((df_col - df_col.mean()) / df_col.std(ddof=0))
outliers = df_col[z_scores > z_thresh]
print(f"{col} - Outliers: {len(outliers)}")
print(outliers, "\n")
z_thresh=3
identify_outliers_with_z_score(df)请记住,在数据集中选择Z-score阈值来识别异常值是一个重要的决策,可以显著影响数据分析的结果。
选择Z-score阈值(通常为1、2或3 )取决于检测异常值所需的敏感度级别和数据的性质。
请记住,Z-score为1涵盖了正态分布曲线下约68%的面积,Z-score为2涵盖了约95%,而Z-score为3涵盖了约99.7%的面积:
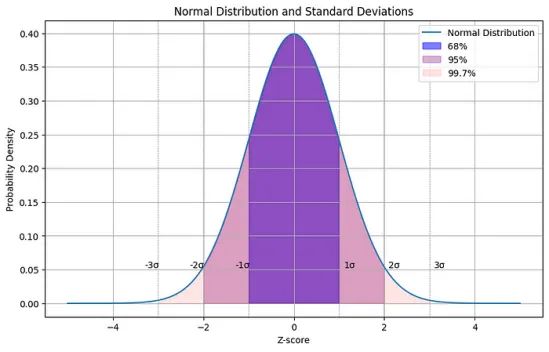
如果你想知道在使用不同类型阈值时,数据中有多少异常值,你也可以绘制它们并进行比较:
def count_outliers_by_z_threshold(series, z_thresholds=[1, 2, 3]):
"""Return counts of outliers for given Z-score thresholds."""
mean = series.mean()
std = series.std()
z_scores = np.abs((series - mean) / std)
# Count outliers for each Z-score threshold
counts = {}
for z_thresh in z_thresholds:
counts[z_thresh] = (z_scores > z_thresh).sum()
return counts
# Assuming 'param_dfs' is your dict of DataFrames
z_thresholds = [1, 2, 3]
outlier_counts_by_threshold = {z: 0 for z in z_thresholds}
for df in param_dfs.values():
for column in df.columns:
series = df[column].dropna() # Drop NaN values
counts = count_outliers_by_z_threshold(series, z_thresholds)
for z_thresh, count in counts.items():
outlier_counts_by_threshold[z_thresh] += count
# Convert counts to a list for plotting
counts = [outlier_counts_by_threshold[z] for z in z_thresholds]
# Plotting
plt.figure(figsize=(8, 6))
bars = plt.bar(z_thresholds, counts, color=['blue', 'orange', 'green'])
plt.xlabel('Z-score Threshold')
plt.ylabel('Number of Outliers')
plt.title('Outliers Count by Z-score Threshold')
plt.xticks(z_thresholds)
# Annotate each bar with its height value
for bar in bars:
yval = bar.get_height()
plt.text(bar.get_x() + bar.get_width()/2, yval + 0.05 * max(counts), int(yval), ha='center', va='bottom')
plt.show()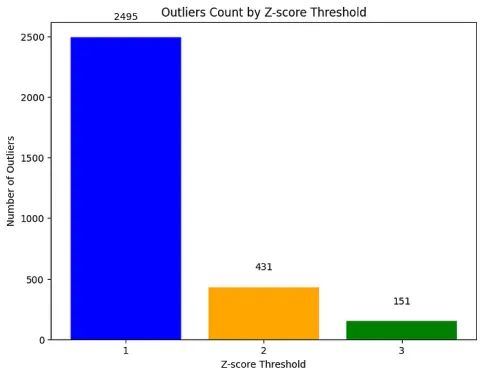
计算不同Z-score阈值的异常值
由于我们处理的是时间序列数据,将异常值的分布按年份进行可视化是很有用的。
df['Z-Score'] = zscore(df['Value'])
# Define outliers based on Z-score greater than 3 or less than -3
df['Outlier'] = (df['Z-Score'] > 3) | (df['Z-Score'] < -3)
# Count outliers per year
outlier_counts = df.resample('Y')['Outlier'].sum().astype(int)
# Reset index to get the year in a separate column and prepare for plotting
outlier_counts = outlier_counts.reset_index()
outlier_counts['Year'] = outlier_counts['index'].dt.year
outlier_counts.drop('index', axis=1, inplace=True)
plt.figure(figsize=(10, 6))
colors = plt.cm.viridis(np.linspace(0, 1, len(outlier_counts)))
plt.bar(outlier_counts['Year'], outlier_counts['Outlier'], color=colors)
plt.title('Distribution of Outliers Per Year')
plt.xlabel('Year')
plt.ylabel('Number of Outliers')
plt.xticks(outlier_counts['Year']) # Ensure all years are shown
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()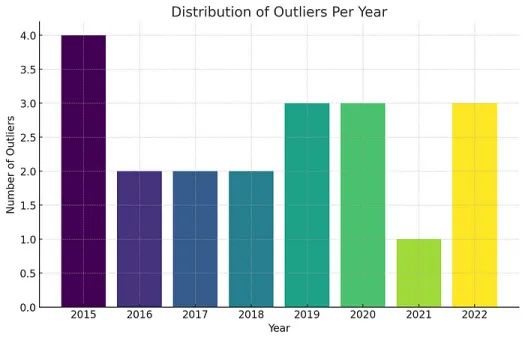
每年异常值的分布
或者按季节:
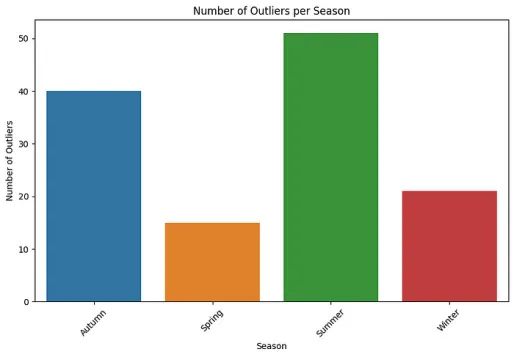
每个季节的异常值分布
稳健的Z-score
也被称为修正后的Z-score方法,通过使用中位数(M)而不是均值来改进传统的Z-score方法,因为均值通常不是最可靠的统计量。此外,它使用中位数绝对偏差(MAD)而不是标准差:
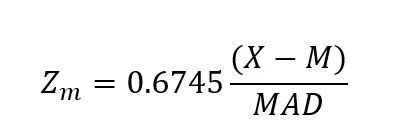
在修正后的Z-score的公式中,0.6745这个因子是用来使MAD的尺度与正态分布中的标准差相当。
这种调整是必要的,因为根据定义,相同数据集的MAD小于标准差。因此,需要调整阈值以适应这种尺度。
注意:中位数和MAD对异常值比均值和标准差更稳健。这种稳健性有时会导致MAD值更小,特别是当异常值极端时。因此,可能需要稍高的阈值(3.5、4甚至5,取决于具体情况)来确保只有最极端的观测值被标记为异常值。
from scipy.stats import median_absolute_deviation
# Calculate modified Z-score using median and median absolute deviation (MAD)
df['Median'] = df['Value'].median()
df['MAD'] = median_absolute_deviation(df['Value'])
df['Modified_Z-Score'] = 0.6745 * (df['Value'] - df['Median']) / df['MAD']
# Define outliers based on modified Z-score greater than 3 or less than -3
df['Outlier'] = (df['Modified_Z-Score'] > 3.5) | (df['Modified_Z-Score'] < -3.5)
# Count outliers per year
outlier_counts = df.resample('Y')['Outlier'].sum().astype(int)
# Reset index to get the year in a separate column and prepare for plotting
outlier_counts = outlier_counts.reset_index()
outlier_counts['Year'] = outlier_counts['index'].dt.year
outlier_counts.drop('index', axis=1, inplace=True)
# Plotting per year
plt.figure(figsize=(10, 6))
colors = plt.cm.viridis(np.linspace(0, 1, len(outlier_counts)))
plt.bar(outlier_counts['Year'], outlier_counts['Outlier'], color=colors)
plt.title('Distribution of Outliers Per Year')
plt.xlabel('Year')
plt.ylabel('Number of Outliers')
plt.xticks(outlier_counts['Year']) # Ensure all years are shown
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()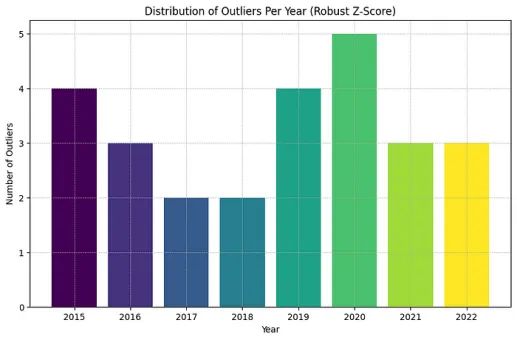
结合统计和可视化方法
让我们在时间序列图中可视化通过Z-score方法(阈值为3)检测到的异常值。
#Here, outliers is a dict
def plot_outliers(df, outliers_dict):
# Number of rows in the subplot will be the number of columns with outliers per stage
for stage, columns_outliers in outliers_dict.items():
# Determine the number of plots
num_plots = len(columns_outliers)
if num_plots == 0:
continue # Skip if no outliers for this stage
# Create subplots
fig, axes = plt.subplots(nrows=num_plots, figsize=(15, num_plots * 5), sharex=True)
fig.suptitle(f'Outlier Visualization for {stage} Stage', fontsize=16)
if num_plots == 1: # If only one plot, wrap it in a list to make iterable
axes = [axes]
for ax, (column, outliers) in zip(axes, columns_outliers.items()):
# Plot the full data series
ax.plot(df.index, df[column], label=f'{column} (Full Series)', color='black', linestyle='-', marker='', alpha=0.5)
# Highlight the outliers
if not outliers.empty:
ax.scatter(outliers.index, outliers, color='red', label='Outliers', marker='o', s=50)
ax.set_title(f'{column} Outliers')
ax.set_ylabel('Values')
ax.legend()
# Set x-axis major locator and formatter
ax.xaxis.set_major_locator(mdates.YearLocator())
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y'))
plt.setp(ax.xaxis.get_majorticklabels(), rotation=45, ha='right')
plt.tight_layout(rect=[0, 0, 1, 0.96]) # Adjust layout
plt.show()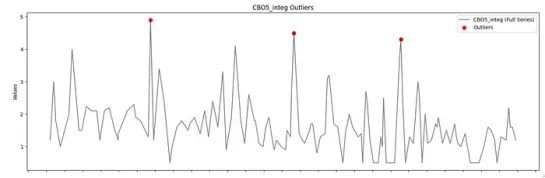
Grubbs检验
Grubbs检验,也称为最大归一化残差检验,通过将数据集中的最大或最小值与数据集的均值和标准差进行比较来识别潜在的异常值。
注意:该检验假设数据遵循单变量正态分布,并且异常值相对于均值和标准差具有极端值。
需要注意的是,Grubb’s 检验通常一次对一个数据点进行,要么针对数据集中的最大值,要么针对最小值。
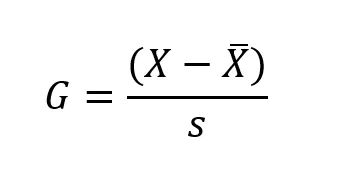
G是Grubbs 检验统计量,X为疑似异常值(数据集中的最大值或最小值),是数据集的均值,s是数据集的标准差。
为了确定可疑的异常值是否显著,可以将计算得到的检验统计量G与适当统计分布(通常是T分布)的临界值进行比较。
如果G超过临界值,则认为可疑异常值具有统计显著性,表明它可能是异常值。
from pyod.models.grubbs import grubbs_test
# Apply Grubbs' test using PyOD
outliers_grubbs = []
for col in df.columns:
outliers = grubbs_test(df[col])
outliers_grubbs.extend([(idx, col) for idx in outliers])
print("Outliers detected by Grubbs' test:")
print(outliers_grubbs)评估指标
为了简短起见,我将通过给出一些例子来提及主要的评估指标。
选择正确的评价指标对于评估异常检测方法的有效性至关重要,尤其是在时间序列分析中。
最佳指标取决于数据的性质、所针对的特定异常以及在假阳性和假阴性之间需要的平衡。
示例:欺诈检测
在欺诈检测中,异常虽然罕见但至关重要,精确率、召回率和F1分数是关键指标。精确率衡量标记为异常的实际异常数。召回率衡量方法正确识别的真实异常数。F1分数在精确率和召回率之间取得平衡,全面评估方法的性能。
示例:预测性维护
对于预测性维护,及时识别异常至关重要。在这种情况下,接收者操作特性(ROC)曲线和曲线下面积(AUC)是常用的指标。这些指标帮助理解真阳性率和假阳性率之间的权衡,这对于优化检测阈值以满足不同的操作需求非常重要。
示例:医疗保健
在医疗保健中,解释性至关重要,因此可视化也同样重要。可视化工具允许领域专家验证检测到的异常,并理解其对决策的影响。通过结合领域知识,这些可视化工具提高了结果的相关性和可解释性,确保检测到的异常既可操作又显著。
选择合适的指标可以显著提高在时间序列数据中检测和管理异常的有效性。
感谢阅读!你还可以订阅我们的YouTube频道,观看大量大数据行业相关公开课:https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ;在LinkedIn上关注我们,扩展你的人际网络!https://www.linkedin.com/company/dataapplab/。
原文作者:Sara Nóbrega
翻译作者:文玲
美工编辑:过儿
校对审稿:Jason
原文链接:https://towardsdatascience.com/the-ultimate-guide-to-finding-outliers-in-your-time-series-data-part-1-1bf81e09ade4





