查找时间序列数据中异常值的终极指南（第2部分）

时间序列分析中异常值检测的有效机器学习方法和工具

异常值：那些可能偏离统计模型、误导预测并扰乱决策过程的数据点。

本文是四篇系列文章中的第二篇，专门讨论时间序列数据中异常值的识别和管理。

本系列的第一篇文章探讨了在时间序列数据中有效识别异常值的视觉和统计方法：

第二篇文章将专门介绍异常值检测的机器学习方法。

鉴于它们的重要性和复杂性，它们值得专门讨论！

第三篇文章探讨了如何管理这些异常值的各种策略，包括移除、保留和封顶技术，并提供了一些处理异常值的实用方法。

在第四篇也是最后一篇文章中，我将继续探讨管理异常值的方法，重点是归算和转换方法，以及评估异常值处理的影响。

在第一篇文章中，我提到了两种不同类型的时间序列数据以及每种数据最适合的离群值检测方法。如果你想了解更多关于时间序列的相关内容，可以阅读以下这些文章：
金融中的机器学习：利用随机森林掌握时间序列分类
关于时间序列分析（TSA），你需要知道这15个词
DeepAR——通过深度学习掌握时间序列预测
Python机器学习库：pycarets新增时间序列模块

当我们正在探索机器学习方法时，有必要回顾一下哪些模型适合单变量和多变量数据。

记住：

单变量数据：这涉及单个变量或随时间变化的特征。重点是在单个时间序列中检测异常。典型的例子包括每日股票价格、每月销售数字或每年的天气数据。

适合于单变量数据的方法往往更简单、更直接。

多变量数据:这涉及多个变量或特征同时。在检测过程中考虑了这些变量之间的关系和相互作用。

例如:一个多变量时间序列可能包括温度、压力、风速的每日测量，所有这些都是同时记录的。

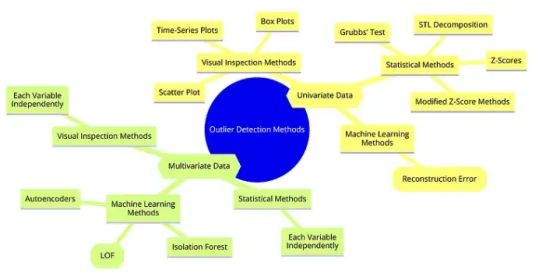
对于具有多个变量的数据，隔离森林、LOF和自动编码器自然适合处理高维数据。我们将在本文中探讨这些方法。

这些机器学习模型，如自动编码器，是多功能工具，不仅限于分析多个变量，因为它们可以适应单变量数据。如何?

想象一下，教一个模型解释单个数据序列的流程。通过将其压缩成更简单的格式，然后尝试重新创建它，模型学习了典型的模式。

当呈现新数据时，原始版本和重建版本之间的显著差异(称为重建错误)充当警报，表明潜在的异常。

数据报告

本文中使用的所有数据集都是合成的，是我专门为这个分析生成的。没有使用外部数据集。

使用机器学习方法的离群值检测

用于异常值检测的隔离林

隔离森林是一种广泛使用的，强大的无监督机器学习算法，用于大型数据集的异常检测。

它之所以引人注目，是因为它采用了独特的方法来隔离异常，而不是识别正常的数据模式。它对于检测大型数据集中的异常值特别有用。

假设：它假设异常值比常规数据点更少，更孤立。

隔离森林构建决策树的集合，并通过识别需要较少分割以在树结构中隔离它们的数据点来隔离异常值。异常值在树中的路径更短，如图2所示。

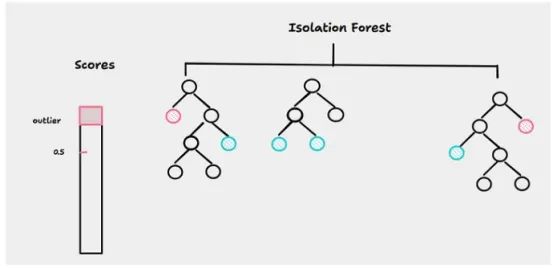
该算法适用于特征空间低维的时间序列数据(相对于观测数而言特征或维数较少)以及离群点分布与规则数据点明显不同的情况。

隔离森林是数据科学家的重要工具，特别是在异常检测领域，让我们逐步了解隔离林的实现。

首先，让我们把数据可视化：

plt.figure(figsize=(10, 6))
plt.plot(summer_data.index, summer_data['Mn_integ'], marker='o', linestyle='-')
plt.title('alc_TA_integ during Summer Season')
plt.xlabel('Date')
plt.ylabel('alc_TA_integ')
plt.xticks(rotation=45)
plt.grid(True)
plt.tight_layout()
plt.show()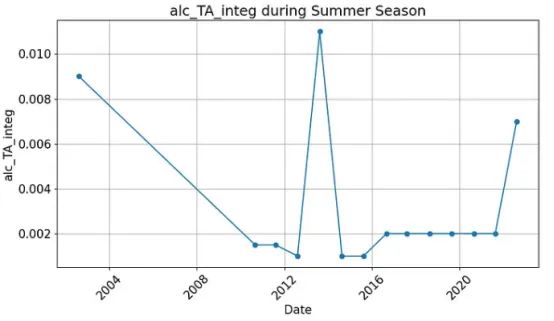

该图显示了在几年的几个夏天测量的大坝化学参数的数据点。

现在，让我们应用隔离森林：

from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import IsolationForest


scaler = StandardScaler()
np_scaled = scaler.fit_transform(values.values.reshape(-1, 1))
data = pd.DataFrame(np_scaled)


outliers_fraction = float(.2)
model =  IsolationForest(contamination=outliers_fraction)
model.fit(data)

关于隔离森林的代码：

• Scikit-learn的StandardScaler用于标准化数据集，确保每个特征的贡献相等，给它一个平均值为零，标准差为1。

这种归一化在时间序列数据中尤其重要，因为时间序列数据的取值范围可能变化很大。fit_transform方法应用于数据，根据算法的需要对其进行重塑。

• 然后创建IsolationForest模型的实例，污染参数设置为0.2。

该参数是对数据集中离群值比例的估计，指导模型预期20%的数据点是异常。

summer_data['anomaly'] = model.predict(data)
fig, ax = plt.subplots(figsize=(10,6))
a = summer_data.loc[summer_data['anomaly'] == -1, ['Mn_integ']]
ax.plot(summer_data.index, summer_data['Mn_integ'], color='black', label = 'Normal')
ax.scatter(a.index,a['Mn_integ'], color='red', label = 'Anomaly')
plt.legend()
plt.show()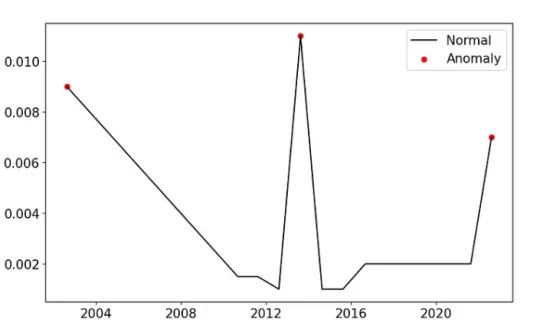

该模型在识别异常数据点方面做得很好！

调整污染参数

污染参数呢?我们如何调整它？

如果观察到大量的真阴性(即，正常数据点被错误地归类为异常)，这表明您的污染参数可能设置得过高。

该参数反映了数据中异常值的预期比例，设置过高会导致许多数据点被错误地分类为正态。

另一方面，如果您看到在您预期的地方缺少红点(表示异常)，则可能意味着污染参数设置得太低。

调整此参数对于识别数据集中的真正异常值至关重要！

离群值检测的先知

你可能听说过这个，因为Prophet是一个著名的时间序列预测模型。

它被设计用来处理时间序列数据并对未来趋势做出预测，但也可以用来检测异常值。

它的工作原理是将时间序列分解为三个主要部分：

• 趋势：捕捉数据在一段时间内的总体方向，说明长期的增加或减少;
• 季节性：模拟周期性波动，如在固定时期内重复的每日、每周或每年的模式。
• 节假日/事件：包括可能影响数据的已知事件或节假日的影响。

我们首先为一个关键指标准备数据，在本例中，与在大坝中测量的化学参数相同，名为“Mn_integ”，捕获夏季数据：

# Prepare the data
df_mn = summer_data[['Date', 'Mn_integ']].rename(columns={'Date': 'ds', 'Mn_integ': 'y'})
# Train the Prophet model for 'Mn_integ'
model_mn = Prophet()
model_mn.fit(df_mn)
# Make predictions for both columns
future_mn = model_mn.make_future_dataframe(periods=0)
forecast_mn = model_mn.predict(future_mn)

在这里，我们将希望预测的特征与时间列“Date”隔离开来。列被重命名为“ds”表示日期，“y”表示特性，这是Prophet模型的要求。

周期参数是什么?

周期参数至关重要，因为它指定了在模型训练期间提供的历史数据范围之外要预测的未来数据点的数量。

设置此参数有助于定义应该为其生成预测的时间范围。

示例:当您将周期设置为0时，表示在历史数据集中的最后一个日期之外不会创建其他未来日期。从本质上讲，该模型只关注为数据中的现有日期生成预测。

这在目标不是预测未来，而是评估模型在已知数据上的性能或检测现有数据集中的异常(就像我们的情况一样!)的场景中特别有用。

plt.figure(figsize=(10, 6))
model_mn.plot(forecast_mn, xlabel='Date', ylabel='Mn_integ', ax=plt.gca())
plt.title('Prophet Forecast for Mn_integ')
plt.show()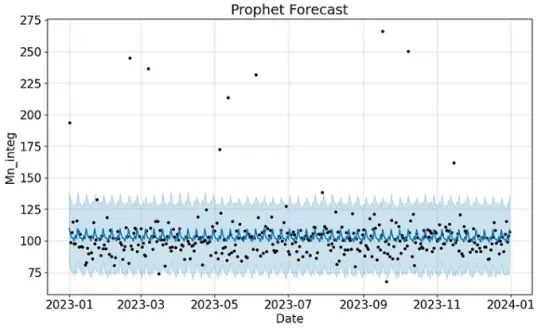

在图5中，该图展示了预测的“Mn_integ”值。该图将实际数据点显示为黑点，预测值显示为蓝线，预测区间显示为蓝色阴影区域，突出显示预测准确性和潜在异常。正如你所看到的，最初的结果非常糟糕。但我们的目标是发现异常，而不是预测。让我们看看，即使在预测很差的情况下，模型也会检测到哪些异常值。

我们该怎么做呢?

注意，第一个代码段中的forecast_mn包含对’ Mn_integ ‘特性的未来预测。但不仅如此。它的组成部分比较多，主要有：

• ds:做出预测的日期。
• yhat:每个日期的“mn_integer”的预测值。
• yhat_lower:预测区间的下界，表示最小期望值。
• yhat_upper:预测区间的上界，表示最大期望值。

我们将利用这些列来检测我们的异常值。

# Merging forecasted data with your original data
forecasting_final_mn = pd.merge(forecast_mn[['ds', 'yhat', 'yhat_lower',
'yhat_upper']], df_mn, how='inner', on='ds')

# Calculate the prediction error and uncertainty
forecasting_final_mn['error'] = forecasting_final_mn['y'] - forecasting_final_mn['yhat']
forecasting_final_mn['uncertainty'] = forecasting_final_mn['yhat_upper'] - forecasting_final_mn['yhat_lower']

# Anomaly detection
factor = 1.5
forecasting_final_mn['anomaly'] = forecasting_final_mn.apply(
lambda x: 'Yes' if (np.abs(x['error']) > factor * x['uncertainty']) else 'No', axis=1
)

为了识别异常，我们可以计算预测误差(y – yhat)和不确定性区间(yhat_upper – yhat_lower)。

然后根据定义的阈值检测异常值：如果绝对误差超过不确定区间的1.5倍，则认为该数据点是异常。

该因子1.5可根据异常检测过程的期望灵敏度进行调整。

import plotly.express as px
# Visualization with Plotly
color_discrete_map = {'Yes': 'rgb(255,12,0)', 'No': 'blue'}
fig = px.scatter(forecasting_final_mn, x='ds', y='y', color='anomaly', title='Anomaly Detection in Mn_integ',
color_discrete_map=color_discrete_map)
fig.show()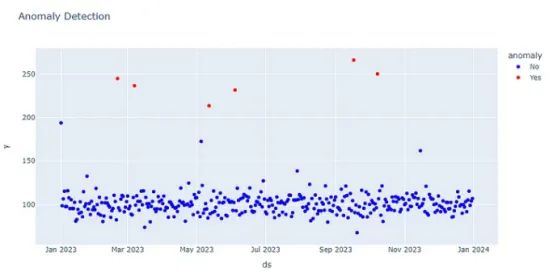

太好了，这个方法发现了一些异常值。请记住，您可以根据您的具体数据和离群值检测需求，通过调整参数，如变化点，节假日，季节性，趋势灵活性和不确定性区间来优化先知模型！

局部异常因子(LOF)

局部异常因子（LOF）因其微妙的异常识别方法而脱颖而出。

这种方法在聚类密度差异较大的数据集中尤为有效。

#Apply LOF Algorithm
lof = LocalOutlierFactor(n_neighbors=20, contamination=0.08)
y_pred = lof.fit_predict(y.reshape(-1, 1))
outlier_scores = lof.negative_outlier_factor_
is_outlier = y_pred == -1

LOF（局部异常因子）首先通过检查每个数据点的局部邻域来工作，该邻域由最近的邻居定义。

这个初始步骤至关重要，因为它为评估一个簇典型的“群体”密度奠定了基础。

n_neighbors指定用于测量局部密度的邻居数量。它是k近邻算法中的“k”。一个典型的起始点是10或20。

如果你增加这个数字，密度估计会变得更加稳定，对单个数据点的敏感度降低，这在含有噪声的数据集中可能有帮助。

如果你减少它，算法会对局部数据结构更加敏感，这在检测密集簇中的异常时可能会有用。

contamination代表预计为异常值的总数据点的比例。如果你认为数据集中有更多的异常值，或者初始结果遗漏了一些潜在的异常值，增加这个值会使算法在标记点为异常值时更具包容性。

plt.figure(figsize=(12, 6))
plt.plot(x, y, 'o', label='Data points')
plt.plot(x[is_outlier], y[is_outlier], 'ro', label='Outliers')
plt.title("Time-Series Data with Outliers Detected by LOF")
plt.xlabel("Time")
plt.ylabel("Value")
plt.legend()
plt.grid(True)
plt.show()
# Output the indices of outliers and their scores for review
outliers_detected = {
"indices": np.where(is_outlier)[0],
"scores": outlier_scores[is_outlier]
}
outliers_detected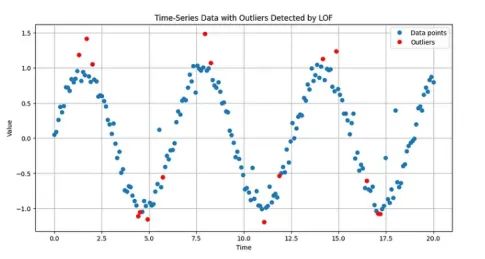

一旦建立了邻域，LOF会计算每个点相对于这个局部群体的密度。

该方法的本质在于将一个点的密度与其邻居的密度进行比较。

一个密度明显低于其邻居的点会被标记为异常值，这表明它是异常点，而不是集群的正常成员。

LOF算法在具有多样化聚类密度的数据集中表现出色。它旨在检测相对于其特定聚类的异常值，使其成为无监督学习场景（数据集未被标记）的强大选择。

然而，使用LOF也并非没有挑战。它对参数设置（如邻居数量）非常敏感；如果设置不当，可能导致检测准确性下降。

此外，由于需要进行大量点对之间的距离计算，LOF在处理较大数据集时可能面临可扩展性问题。

基于聚类的异常检测

关于这些方法，我可以写整篇文章。在这里，我将简要提及一些常见的方法及其在时间序列异常检测中的应用。

每种方法都有其独特的特点，适用于不同类型的数据和分析目标。

分区方法通过优化标准（如最小化簇内距离）将数据划分为特定数量的簇，K-means就是一个经典的例子。

对于时间序列数据，这通常涉及将数据转换为合适的格式，如表示时间序列片段的特征向量，或使用主成分分析（PCA）等降维技术。

这种方法最适合具有球形簇的大型数据集，其中簇的数量是已知的，并且这些方法在计算上效率高且易于实现。

然而，它们对初始质心位置非常敏感，并且在处理不同大小和密度的簇时存在困难。在时间序列中，定义合适的特征和处理时间依赖性是一个挑战。

# Transform time-series data into feature vectors using a sliding window approach
window_size = 10
X = np.array([amplitude[i:i+window_size] for i in range(len(amplitude) - window_size)])

# Standardize the data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Apply K-means clustering
n_clusters = 3
kmeans = KMeans(n_clusters=n_clusters, random_state=42)
labels = kmeans.fit_predict(X_scaled)

# Prepare data for visualization
# We'll plot the first point in each window
time_plot = time[:len(labels)]
amplitude_plot = amplitude[:len(labels)]

# Visualize the clusters
plt.figure(figsize=(12, 6))
colors = ['blue', 'green', 'red']
for i in range(n_clusters):
plt.scatter(time_plot[labels == i], amplitude_plot[labels == i], color=colors[i], label=f'Cluster {i}')
plt.scatter(time[outlier_indices], amplitude[outlier_indices], color='gold', edgecolor='black', s=100, label='Outliers')
plt.title("Time-Series Data Clustering with K-means")
plt.xlabel("Time")
plt.ylabel("Value")
plt.legend()
plt.grid(True)
plt.show()

# Check cluster centers
cluster_centers = kmeans.cluster_centers_
print("Cluster Centers (Scaled):", cluster_centers)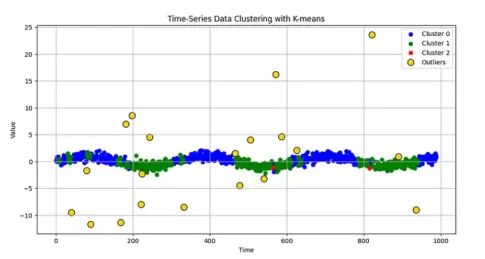

分层法无需预先指定聚类的数量，即可建立聚类树。

这种方法在聚类结构未知的情况下非常有用，可以聚合（建立聚类），也可以分割（分解聚类）。

这些方法通过树枝图提供直观的可视化效果，但对计算要求较高，这可能会限制其在大型数据集上的应用。

举例说明：聚合聚类

聚合聚类是一种分层聚类方法。它是最常用的分层聚类技术之一，尤其适用于将数据转换为合适格式后识别时间序列数据中的嵌套聚类。

import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.cluster import AgglomerativeClustering
from sklearn.preprocessing import StandardScaler

# Transform time-series data into feature vectors using a sliding window approach
window_size = 10
X = np.array([amplitude[i:i+window_size] for i in range(len(amplitude) - window_size)])

# Standardize the data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Step 1: Use Agglomerative Clustering
linked = linkage(X_scaled, method='ward')

# Step 2: Plot Dendrogram to determine the optimal number of clusters
plt.figure(figsize=(12, 6))
dendrogram(linked, orientation='top', distance_sort='descending', show_leaf_counts=True)
plt.title('Dendrogram for Hierarchical Clustering')
plt.xlabel('Time Series Segments')
plt.ylabel('Euclidean Distance')
plt.show()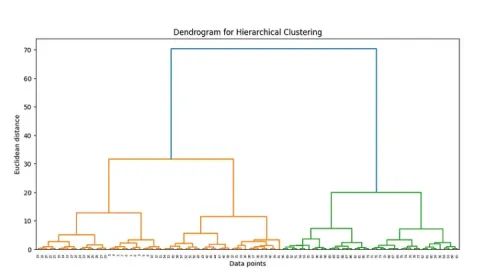

图9中的树状图展示了分层聚类过程的表示。它展示了如何基于它们之间的欧氏距离逐步将个体数据点合并成簇。根据树状图的分析，选择一个截断距离，以得到一个合理聚类数量（在这种情况下是3个）。

树枝图的纵轴代表聚类合并时的距离。距离越大，说明聚类之间的相似性越低。

# Choosing a cutoff (distance) that results in a sensible number of clusters
#From the dendogram, 3 clusters
agg_clustering = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='ward')
labels_agg = agg_clustering.fit_predict(X_scaled)

# Prepare data for visualization
# We'll plot the first point in each window
time_plot = time[:len(labels_agg)]
amplitude_plot = amplitude[:len(labels_agg)]

# Step 3: Visualization of Clusters
plt.figure(figsize=(12, 6))
colors = ['blue', 'green', 'red']
for i in range(3):
plt.scatter(time_plot[labels_agg == i], amplitude_plot[labels_agg == i], color=colors[i], label=f'Cluster {i}')
plt.scatter(time[outlier_indices], amplitude[outlier_indices], color='gold', edgecolor='black', s=100, label='Outliers')
plt.title("Time-Series Data Clustering with Agglomerative Hierarchical Clustering")
plt.xlabel("Time")
plt.ylabel("Value")
plt.legend()
plt.grid(True)
plt.show()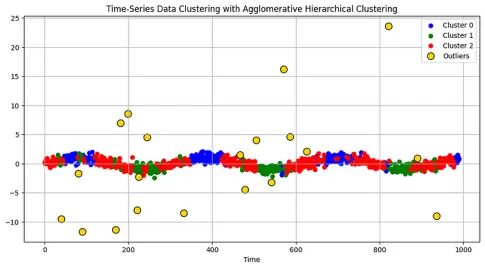

让我们检查一下代码部分。

n_clusters指定要找到的聚类数目。这决定了聚类过程结束时预期的聚类数目。

要优化n_clusters，可以使用树枝图来直观地识别自然的聚类划分，应用肘部法在聚类紧凑性和数量之间找到平衡，或者计算轮廓系数以确定将数据分离成不同组的最佳聚类配置。

基于密度的方法将聚类确定为密度高于数据其他部分的区域，将稀疏区域视为噪声或边界点，其中DBSCAN是一种常用算法。

这些方法能很好地处理不规则或相互交织的聚类，并对噪声和异常值具有强大的抗干扰能力。不过，它们的有效性取决于对密度定义参数的准确设置，而这些参数会随着数据密度的变化而变化。

DBSCAN的工作原理是将时间序列数据转换到合适的特征空间，如使用滑动窗口、特征提取或嵌入技术。它可以识别相似模式的聚类，并将明显偏离这些聚类的点检测为异常值。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler

# Create a synthetic dataset with different parameters
data, _ = make_blobs(n_samples=350, centers=4, cluster_std=1.0, random_state=24)

# Introduce some outliers
outliers = np.random.uniform(low=-12, high=12, size=(25, 2))
data = np.vstack([data, outliers])

# Standardize the dataset
scaler = StandardScaler()
data = scaler.fit_transform(data)

# Apply DBSCAN with different parameters
epsilon = 0.35
min_pts = 8
dbscan = DBSCAN(eps=epsilon, min_samples=min_pts)
dbscan.fit(data)

min_samples参数降低了对聚类密度的要求，允许更多的点成为核心点，从而产生更多的聚类，包括较小或密度较低的聚类。

DBSCAN中的eps（epsilon）参数定义了两点之间被视为同一邻域（簇）的最大距离。要调整这个参数，通常可以从小值开始，然后逐渐增大，检查它对聚类数量和质量的影响，力求在过多的小聚类和过少的大聚类之间取得平衡。

# Apply DBSCAN
epsilon = 2.8 # Increase epsilon to include more points in each cluster
min_samples = 3 # Decrease min_samples to allow smaller clusters

dbscan = DBSCAN(eps=epsilon, min_samples=min_samples)
labels = dbscan.fit_predict(windows_scaled)


# Identify outlier indices
outlier_indices = np.where(labels == -1)[0]

# Convert outlier indices to the corresponding time points
outlier_time_indices = np.array([i + window_size // 2 for i in outlier_indices])

# Plot the time series data with detected outliers
plt.figure(figsize=(12, 6))
plt.plot(time, data, label='Time Series Data')
plt.scatter(time[outlier_time_indices], data[outlier_time_indices], color='red', label='Detected Outliers', marker='x')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()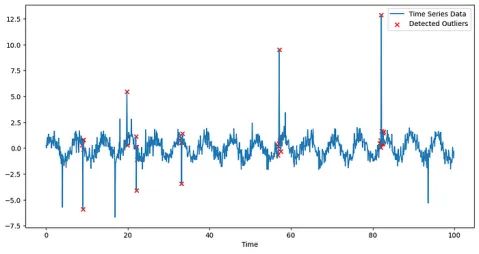

DBSCAN成功识别了一些异常值，但从图11中可以看出，可能存在一些误报。

该模型的有效性在很大程度上取决于参数（eps和min_samples）的正确设置。请务必根据自己的需要调整这些参数！

最后，基于网格的方法可以通过将时间维度离散化为时间间隔，有效地沿着时间轴创建网格，从而适用于时间序列数据。

这种方法对于高维时间序列数据非常有利，可以实现高效处理和并行化。不过，这些方法对时间序列进行聚类的有效性在很大程度上取决于所选时间间隔的粒度，在处理不同密度的时间序列模式时可能会遇到困难。

因此，虽然这些方法能提供高效的处理，但其实现可能很复杂，可能需要自定义才能有效处理时间序列应用中的各种模式。鉴于其复杂性，我就不在此举例说明了。

自动编码器（Autoencoders）

自动编码器是一类用于无监督学习的神经网络，特别用于学习数据的高效表示或编码。

有几种利用自编码器在时间序列数据中进行异常检测的方法。这里，我将举例说明其中一种方法：

原始自动编码器（Vanilla Autoencoder）

基础自编码器由两个主要组件组成—编码器和解码器。编码器将时间序列数据压缩成潜在空间表示，而解码器从这种压缩形式重构原始数据。

import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, Dense

# Normalize data
amplitude = (amplitude - np.mean(amplitude)) / np.std(amplitude)

# Reshape for input to autoencoder (time steps, features)
amplitude = np.expand_dims(amplitude, axis=-1)

# Define autoencoder model
input_layer = Input(shape=(amplitude.shape[1],))
encoded = Dense(32, activation='relu')(input_layer)
decoded = Dense(amplitude.shape[1], activation='linear')(encoded)

autoencoder = Model(input_layer, decoded)
autoencoder.compile(optimizer='adam', loss='mse')

# Train the autoencoder
autoencoder.fit(amplitude, amplitude,
epochs=50,
batch_size=32,
shuffle=True,
validation_split=0.2)

# Predict on the entire dataset
reconstructed_data = autoencoder.predict(amplitude)

# Calculate Mean Squared Error (MSE) as reconstruction error
mse = np.mean(np.power(amplitude - reconstructed_data, 2), axis=1)

# Set a threshold for outlier detection
threshold = np.percentile(mse, 95) # Adjust percentile as needed

# Identify outliers
outliers = np.where(mse > threshold)[0]

该代码首先通过减去平均值并除以标准差对数据进行归一化处理，然后对数据进行重塑，使其符合自动编码器预期的输入格式。它使用TensorFlow/Keras定义并训练Vanilla自动编码器，计算原始数据与重建数据之间的均方误差(MSE)，以识别异常值，最后根据MSE值第95个百分位数设置的阈值检测异常值。

import matplotlib.pyplot as plt

# Plot original and reconstructed data
plt.figure(figsize=(14, 7))
plt.plot(amplitude, label='Original Data', color='blue')
plt.plot(reconstructed_data, label='Reconstructed Data', color='red', linestyle='--')
plt.title('Original vs Reconstructed Data')
plt.xlabel('Time Steps')
plt.ylabel('Amplitude')
plt.legend()
plt.grid(True)
plt.show()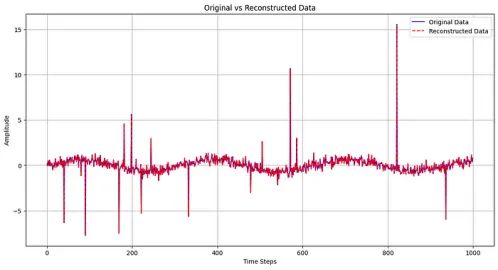

图12中的图直观地比较了原始时间序列数据（蓝线）和自动编码器重建的数据（红色虚线），显示了自动编码器对原始数据中存在的模式和异常的捕捉程度。

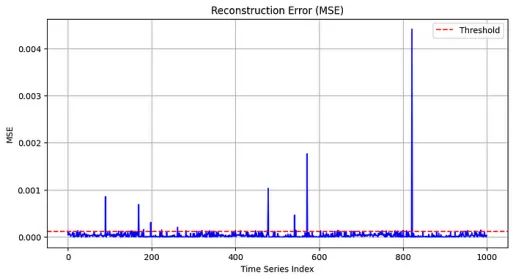
图13显示了时间序列各指数的MSE。红色虚线表示用于异常值检测的阈值。高于该阈值的点可能表示数据中存在潜在的异常或异常值。

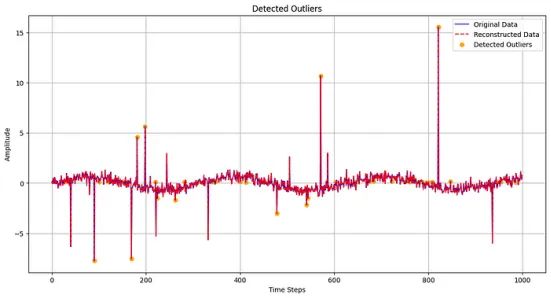
最后，在图14中，将原始数据（蓝线）和重建数据（红色虚线）叠加在一起，检测到的异常值突出显示为橙色点。它直观地识别了自动编码器根据重建误差超过设定阈值而识别出异常的特定时间步骤。

总结

就是这样！感谢您的阅读。

在本文中，我们探讨了一系列用于检测时间序列数据中异常值的机器学习方法，包括Isolation Forest、Prophet、LOF、基于聚类的方法和自动编码器。

每种方法都有其独特的优势，因此根据具体的数据特征和分析需求选择合适的工具至关重要。

请继续关注第3部分，我将探讨管理这些异常值的几种策略，重点是减轻异常值对数据分析影响的转换技术和实用解决方案。

你在时间序列分析中常用哪些机器学习方法？你还知道哪些其他方法？请留言告诉我。

感谢阅读！你还可以订阅我们的YouTube频道，观看大量大数据行业相关公开课：https://www.youtube.com/channel/UCa8NLpvi70mHVsW4J_x9OeQ；在LinkedIn上关注我们，扩展你的人际网络！https://www.linkedin.com/company/dataapplab/。

原文作者：Sara Nóbrega
翻译作者：文玲
美工编辑：过儿
校对审稿：Jason
原文链接：https://towardsdatascience.com/the-ultimate-guide-to-finding-outliers-in-your-time-series-data-part-2-674c25837f29